По теореме Пифагора
надо или мне поставят 2 за четверть​

Номер 524 (б, в , г)

б) •90°= 90π/180= π/2

•120°= 120π/180= 2π/3

•135°= 135π/180= 27π/36= 3π/4

•150°= 150π/180= 15π/18= 5π/6

в) •210°= 210π/180= 7π/6

•225°= 225π/180= 45π/36= 5π/4

•270°= 270π/180= 3π/2

•300°= 300π/180= 10π/6= 5π/3

г) •1100°= 1100π/180= 110π/18= 22π/9

•1440°= 1440π/180= 144π/18= 16π/2= 8π

•3330°= 3330π/180= 333π/18= 37π/2

•7380°= 7380π/180= 738π/18= 41π

Номер 525(б, в, г)

б) • - (3π/2)= - (3π/2)× 180/π= - (3×180÷2)= -270°

•π/12= π/12 × 180/π= 180/12= 15°

•4π/9= 4π/9 × 180/π= 4×180÷9= 80°

•-3π= -3π × 180/π= - 540°

в) • -π= -180°

• π/18= π/18 × 180/π= 10°

• -⅚π= - (5π/6) × (180/π)= - (5×180÷6)= -150°

•π/36= 5°

г) Когда даны только цифры в радианы, у нас принято умножать на 57°(возможно, у вас другие правила)

• 2= 2×57= 114°

• -3= -3×57= -171°

• 2,5= 2,5×57°= 142,5°

• -15= -15×57= -855°.

Номер 526(г, д, е)

Отсчет угла ведется строго от нуля: против часовой если угол положительный, по часовой — если отрицательный.

г) β= -1040°

Отрицательный угол, по часовой.

-1040= -360-360-320.

То есть можно сказать, что -1040= -320.

-320 — это первая четверть.

д) β=2900°

Угол положительный, против часовой.

2900= 360×8+20.

2900=20

20 — это первая четверть.

е) β= -3750°

-3750= -360×10-150

-3750= -150

-150 — это третья четверть.

Давайте для начала формализуем условие. У насть есть вероятностное простравнство Ω. Что такое в нём исход? Исход - это как раз передача сообщения n раз. Исход можно закодировать последовательностью n+1 чисел. Каждое число в последовательности обозначает жителя, а следующее жителя которому будет передано сообщение. Получаем, что:

Из условия следует, что каждый исход равновероятен.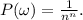

Теперь посчитаем вероятность, что новость будет передана n раз без повторного сообщения её кому-нибудь. Обозначим это событие как A. Заметим, что каждый благоприятный исход (лежит в А) представляет собой перестановку (n+1)-го чисел. Всего таких перестановок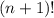 . Теперь можно считать вероятность: