Область определения находить очень просто. Проверяем, накладывается ли какое-либо граничение на функцию: если функция представляет собой дробь,то знаменатель не должен быть равен нулю; если в функции присутствует корень, то подкоренное выражение должно быть больше либо равно нулю; если в функции присутствует логарифм, то там ограничения согласно определению логарифма.
Затем, найдя область определения (какие значения может принимать х), смотрим, какие значения может принимать у на данной области определения. Это и будет множество значений функции
кубическая функция может иметь только локальный минимум. Потому что при х -> она уходит в
точки минимума и максимума соответствуют нулям производной
сумма степеней равна нулю, значит один корень = 1, второй = a
локальным минимумом является больший корень (кубическая функция возрастает от минус бесконечности до первого корня, потом убывает, потом снова возрастает до плюс бесконечности)
значит при a<1 локальный минимум f(x=1) = 1/3 - (a+1)/2 + a - 7 = a/2 - 7
Область определения находить очень просто. Проверяем, накладывается ли какое-либо граничение на функцию: если функция представляет собой дробь,то знаменатель не должен быть равен нулю; если в функции присутствует корень, то подкоренное выражение должно быть больше либо равно нулю; если в функции присутствует логарифм, то там ограничения согласно определению логарифма.
Затем, найдя область определения (какие значения может принимать х), смотрим, какие значения может принимать у на данной области определения. Это и будет множество значений функции
кубическая функция может иметь только локальный минимум. Потому что при х ->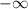
она уходит в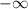 
точки минимума и максимума соответствуют нулям производной
сумма степеней равна нулю, значит один корень = 1, второй = a
локальным минимумом является больший корень (кубическая функция возрастает от минус бесконечности до первого корня, потом убывает, потом снова возрастает до плюс бесконечности)
значит при a<1 локальный минимум f(x=1) = 1/3 - (a+1)/2 + a - 7 = a/2 - 7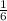
при а>1 локальный минимум f(x=a) = a^3/3-(a+1)/2*a^2+a^2 - 7 = (1/3 - 1/2) a^3 + (-1/2+1) a^2 - 7 = - a^3 / 6 + a^2 / 2 - 7
при a = 1 имеем точку перегиба и никакого минимума