Основанием четырехугольной пирамиды служит квадрат. Одно из боковых ребер перпендикулярно плоскости основания. Какую длину должна иметь высота пирамиды, чтобы радиус шара, описанного около пирамиды, был наименьшим, если объем пирамиды равен 72? 300б за решение

1)  

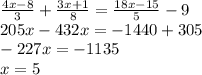
ответ: 5

ответ : x принадлежит R

2) ответ: нет решений, т.к. графики не пересекаются

3) Составим таблицу:

                            1 раствор     2 раствор    смесь

 концентрация       8 %             16%              11%

   масса                    х мл             у мл          400 мл

масса соли           х*8/100           у*16/100      400*11/100

Тогда получим два уравнения

х+у=400

0,08х+0,16у=44

Решим полученную систему:

Вычтем из второго уравнения первое:

8x+16y-8x-8y=4400-3200

8y=1200

y=150 мл

Тогда х= 400-150=250 мл

ответ: Первого раствора 250 мл, второго 150 мл

1. С, так как накрест лежащие углы равны

2. Внешний угол треугольника равен сумме двух других углов, не смежных с ним

получается 2х+3х=100°

5х=100°

х=20°

2х=2*20=40° - угол С

3. Сумма углов треугольника равна 180

Получается угол В = 180-(54+84)=42°

Так как  СС₁ - биссектриса, то угол АСС₁=С₁СВ=84:2=42

Рассмотри ΔСС₁В:

получается ∠С₁СВ=∠С₁ВС=42°⇒ΔСС₁В - равнобедренный⇒ С₁С=С₁В=10

4. АК - гипотенуза, равна 12

АС - катет, равный половине гипотенузы(6)⇒лежит напротив угла в 30°, т.е. ∠К=30°

180-(90+30)=60° - ∠А

Ну а так как СМ - высота, то образуется два прямоугольных треугольника АМС и СМК

ΔАМС:

∠АСМ=180-(90+60)=30°

ΔСМК:

∠МСК=180-(90+30)=60°