Основание прямой призмы - прямоугольный треугольник с катетами 3см и 4см. высота призмы равна 4см. Найти объем и площадь полной поверхности призмы. УМОЛЯЮ ОЧЕНЬ
Решим уравнение в зависимости от значений параметра (постоянной)
Применим классическое решение уравнения типа
1) Найдем те значения , при которых обнуляются модули - это и
2) Выставим на координатной оси эти значения:
3.1) Рассмотрим промежуток :
Выясним значение выражений подмодульных выражений:
Раскроем данные модули. Если подмодульное выражение меньше нуля, то для того чтобы его раскрыть, нужно изменить знак выражение, тем самым модуль раскроется с неотрицательным выражением.
Если , то , что верно при любых из рассматриваемого промежутка
Если , то
3.2. Рассмотрим промежуток :
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если , то , что верно при любых из рассматриваемого промежутка
Если , то
Однако, 3 не входит в данный интервал, который мы рассматриваем.
3.3. Рассмотрим промежуток :
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если , то , что неверно ни при каких
Если , то
Рассмотрим данный ответ на заданном интервале. Этот ответ нам подойдет, если выполниться условие:
ответ: прямоугольные равнобедренные треугольники; Может быть из квадратов..
Объяснение:
С изображение сложности, поэтому попытаюсь словами объяснить.
Множество тупоугольных треугольников и множество равнобедренных треугольников входят в множество всех треугольников. То есть чертим круг и внутри его размещаем два круга меньшим размером. Только эти два круга внутри должны пересекаться, так как тупоугольные треугольники могут быть равнобедренными, а равнобедренные треугольники могут быть тупоугольными.
Решим уравнение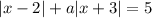 в зависимости от значений параметра (постоянной)
в зависимости от значений параметра (постоянной) 
Применим классическое решение уравнения типа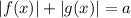
1) Найдем те значения , при которых обнуляются модули - это
, при которых обнуляются модули - это 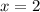 и
и 
2) Выставим на координатной оси эти значения:
эти значения:
3.1) Рассмотрим промежуток![x \in (-\infty; -3]](/tpl/images/1025/4528/6d9ac.png) :
:
Выясним значение выражений подмодульных выражений:
Раскроем данные модули. Если подмодульное выражение меньше нуля, то для того чтобы его раскрыть, нужно изменить знак выражение, тем самым модуль раскроется с неотрицательным выражением.
Если , то
, то  , что верно при любых
, что верно при любых  из рассматриваемого промежутка
из рассматриваемого промежутка
Если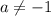 , то
, то 
3.2. Рассмотрим промежуток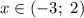 :
:
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если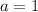 , то
, то  , что верно при любых
, что верно при любых  из рассматриваемого промежутка
из рассматриваемого промежутка
Если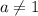 , то
, то 
Однако, 3 не входит в данный интервал, который мы рассматриваем.
3.3. Рассмотрим промежуток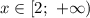 :
:
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если , то
, то 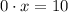 , что неверно ни при каких
, что неверно ни при каких 
Если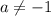 , то
, то 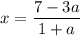
Рассмотрим данный ответ на заданном интервале. Этот ответ нам подойдет, если выполниться условие:
Решим данное неравенство методом интервалов:
1)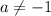
2)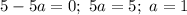
Отметим данные точки на координатной оси
Таким образом,![a \in (-1; \ 1]](/tpl/images/1025/4528/68d76.png)
Еслиответ: прямоугольные равнобедренные треугольники; Может быть из квадратов..
Объяснение:
С изображение сложности, поэтому попытаюсь словами объяснить.
Множество тупоугольных треугольников и множество равнобедренных треугольников входят в множество всех треугольников. То есть чертим круг и внутри его размещаем два круга меньшим размером. Только эти два круга внутри должны пересекаться, так как тупоугольные треугольники могут быть равнобедренными, а равнобедренные треугольники могут быть тупоугольными.
K∪(I∩М)