Площадь фигуры ограниченной линиями f(x)=x+5, g(x)=6/x, x=-2, x=6 и осью 0x равна (16,5 +6 ln6) ед.²
Объяснение:
Требуется найти площадь фигуры ограниченной линиями f(x)=x+5, g(x)=6/x, x=-2, x=6 и осью 0x.
Площадь фигуры найдем по формуле:
Дано:
Построим графики и определим область, которая ограничена данными линиями.
1.
-линейная функция, график прямая.
Для построения достаточно две точки:
х = -5, у=0;
х = 1, у=6.
Строим график.
2.
-функция обратной пропорциональности, график гипербола, расположенная в первой и третьей четвертях.
Возьмем четыре точки:
х = 1, у = 6;
х = 2, у = 3;
х = 3, у = 2;
х = 6, у = 3.
Строим одну ветвь гиперболы. Вторую строим симметрично начала координат.
3. Точки пересечения данных графиков:
(1; 6) и (-6; -1).
4. Видим, что искомая площадь состоит из двух площадей:
5. Найдем S₁.
Линия сверху f₂(x) = x+5, снизу f₁(x) = 0, слева b = -2, справа a = 1.
6. Найдем S₂.
f₂(x) = 6/x, f₁(x) = 0, b = 1, a = 6.
7. S = S₁ +S₂ = 13,5 + 6 ln6 (ед²)
найду координаты точки пересечения диагоналей О-это середина АС
координата х : (-2+4)/2=1
y: (-4+2)/2=-1
z: (5+(-3))/2=1
O(1;-1;1)
пусть координаты четвертой вершины параллелограмма D (x;y;z)
тогда О-середина BD
распишу координаты О через B и D
по х: 1=(-1+x)/2; -1+x=2; x=3
y: -1=(4+y)/2; 4+y=-2;y=-6
z: 1=(2+z)/2; 2+z=2;z=0
D(3;-6;0)
Теперь осталось найти cos<AOB в треугольнике АОВ по т косинусов, предварительно посчитав его стороны
AO²=(1-(-2))²+(-1+(-4))²+(1-5)²=9+25+16=50; AO=5√2
AB²=(-1+2)²+(4+4)²+(2-5)²=1+64+9=74; AB=√74
BO²=(1+1)²+(-1-4)²+(1-2)²=4+25+1=30; BO=√30
тогда по т косинусов
AB²=AO²+AB²-2*AO*BO*cos<AOB
74=50+30-2*5√2*√30*cos<AOB
cos<AOB=6/(10√60)≈0.077-почти прямой угол
Площадь фигуры ограниченной линиями f(x)=x+5, g(x)=6/x, x=-2, x=6 и осью 0x равна (16,5 +6 ln6) ед.²
Объяснение:
Требуется найти площадь фигуры ограниченной линиями f(x)=x+5, g(x)=6/x, x=-2, x=6 и осью 0x.
Площадь фигуры найдем по формуле:
Дано:
Построим графики и определим область, которая ограничена данными линиями.
1.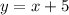
-линейная функция, график прямая.
Для построения достаточно две точки:
х = -5, у=0;
х = 1, у=6.
Строим график.
2.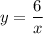
-функция обратной пропорциональности, график гипербола, расположенная в первой и третьей четвертях.
Возьмем четыре точки:
х = 1, у = 6;
х = 2, у = 3;
х = 3, у = 2;
х = 6, у = 3.
Строим одну ветвь гиперболы. Вторую строим симметрично начала координат.
3. Точки пересечения данных графиков:
(1; 6) и (-6; -1).
4. Видим, что искомая площадь состоит из двух площадей:
5. Найдем S₁.
Линия сверху f₂(x) = x+5, снизу f₁(x) = 0, слева b = -2, справа a = 1.
6. Найдем S₂.
f₂(x) = 6/x, f₁(x) = 0, b = 1, a = 6.
7. S = S₁ +S₂ = 13,5 + 6 ln6 (ед²)
найду координаты точки пересечения диагоналей О-это середина АС
координата х : (-2+4)/2=1
y: (-4+2)/2=-1
z: (5+(-3))/2=1
O(1;-1;1)
пусть координаты четвертой вершины параллелограмма D (x;y;z)
тогда О-середина BD
распишу координаты О через B и D
по х: 1=(-1+x)/2; -1+x=2; x=3
y: -1=(4+y)/2; 4+y=-2;y=-6
z: 1=(2+z)/2; 2+z=2;z=0
D(3;-6;0)
Теперь осталось найти cos<AOB в треугольнике АОВ по т косинусов, предварительно посчитав его стороны
AO²=(1-(-2))²+(-1+(-4))²+(1-5)²=9+25+16=50; AO=5√2
AB²=(-1+2)²+(4+4)²+(2-5)²=1+64+9=74; AB=√74
BO²=(1+1)²+(-1-4)²+(1-2)²=4+25+1=30; BO=√30
тогда по т косинусов
AB²=AO²+AB²-2*AO*BO*cos<AOB
74=50+30-2*5√2*√30*cos<AOB
cos<AOB=6/(10√60)≈0.077-почти прямой угол