В итоге,существует расставить 2 ученикам 2 оценки (4 и 5).
А если прибавить к ним еще одного ученика - С. То:
А Б С 4 4 4 5 5 5 4 4 5 4 5 5 5 5 4 5 4 4 4 5 4 5 4 5
В итоге получаем
А что если, оставим тех же 2 учеников, но добавим 1 оценку - 3?
А вот что получим:
А Б 3 3 4 4 5 5 3 4 4 3 4 5 5 4 3 5 5 3
В итоге, мы получили
Нет смысла, добавлять 3 ученика. Уже и так можно увидеть закономерность.
В 1 раз, мы имели 2 ученика и 2 оценки, отметим это как: В 2 раз, мы имели 3 ученика и 2 оценки, отметим это как: В 3 раз, мы имели 2 ученика и 3 оценки, отметим это как:
А теперь, выведем формулу: - где a-число оценок, b-число учеников.
В итоге и получаем: 1 случай: 2 случай: 3 случай:
Теперь, вычислим наш случай в задаче. Есть 24 ученика = b, и 4 оценки=a (2,3,4,5). Отсюда:
Второй
Для первого ученика существует 4 варианта: 2,3,4,5 Для второго ученика существует 4 варианта на каждый вариант первого ученика. То есть: - варианта событий.
Для третьего ученика существует 4 варианта на каждый вариант второго ученика. То есть: - варианта событий.
И так далее. В итоге получаем, что для 24 учеников существует ровно:
1 ученик - А
2 ученик - Б
Получаем:
А Б
4 5
5 4
5 5
4 4
В итоге,существует расставить 2 ученикам 2 оценки (4 и 5).
А если прибавить к ним еще одного ученика - С. То:
А Б С
4 4 4
5 5 5
4 4 5
4 5 5
5 5 4
5 4 4
4 5 4
5 4 5
В итоге получаем
А что если, оставим тех же 2 учеников, но добавим 1 оценку - 3?
А вот что получим:
А Б
3 3
4 4
5 5
3 4
4 3
4 5
5 4
3 5
5 3
В итоге, мы получили
Нет смысла, добавлять 3 ученика. Уже и так можно увидеть закономерность.
В 1 раз, мы имели 2 ученика и 2 оценки, отметим это как:
В 2 раз, мы имели 3 ученика и 2 оценки, отметим это как:
В 3 раз, мы имели 2 ученика и 3 оценки, отметим это как:
А теперь, выведем формулу:
В итоге и получаем:
1 случай:
2 случай:
3 случай:
Теперь, вычислим наш случай в задаче. Есть 24 ученика = b, и 4 оценки=a (2,3,4,5).
Отсюда:
Второй
Для первого ученика существует 4 варианта:
2,3,4,5
Для второго ученика существует 4 варианта на каждый вариант первого ученика.
То есть:
Для третьего ученика существует 4 варианта на каждый вариант второго ученика.
То есть:
И так далее. В итоге получаем, что для 24 учеников существует ровно:
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение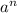
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение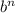
.
Рассмотрим многочлен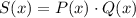
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена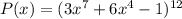
:
- степень определяется выражением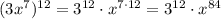
, то есть степень равна 84
- свободный член равен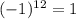
Для многочлена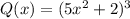
:
- степень определяется выражением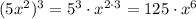
, то есть степень равна 6
- свободный член равен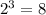
Наконец, для многочлена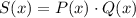
получим:
- степень определяется выражением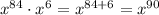
, то есть степень равна 90
- свободный член равен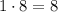
Сумма степени и свободного члена многочлена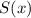
:
ответ: 98