Алгебра: Объясните , как это решать! Алгебра 8 класс.

Объясните , как это решать! Алгебра 8 класс.

Показать ответ

Ответ:

vanyushagay96

06.01.2022 06:00

2х-1/(2х+1) - (2х+1)/(2х-1) + 4/(2х-1)(2х+1)=0

(2х-1)² - (2х+1)²=-4

(2х-1+2х+1)(2х-1-2х-1)=-4

4х*(-2)=-4

х=-4/-8

х=1/2.

Не ∈ ОДЗ

Корней нет.

0,0(0 оценок)

Ответ:

Пони0с0радушкой

06.01.2022 06:00

Само решение написано с красной строки, остальное (кроме ОДЗ) - пояснения.

ОДЗ: т.к. знаменатель не равен 0,

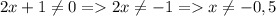
1) $2x+1\neq 0 = 2x\neq -1=x\neq -0,5$

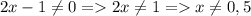
2) $2x-1\neq 0=2x\neq 1=x\neq 0,5$

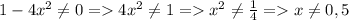
3) $1-4x^2\neq 0 = 4x^2\neq 1= x^2\neq \frac{1}{4}=x\neq 0,5$

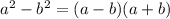Здесь задание на применение формулы разности квадратов, которая выглядит следующим образом: a^2-b^2=(a-b)(a+b) .

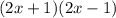$\frac{2x-1}{2x+1}=\frac{2x+1}{2x-1}+\frac{4}{1-4x^2}$

Перенесем все для удобства в левую часть.

$\frac{2x-1}{2x+1}-\frac{2x+1}{2x-1}-\frac{4}{1-4x^2}=0$

Теперь приведем две первые дроби к общему знаменателю (2x+1)(2x-1) .

$\frac{(2x-1)(2x-1)}{(2x+1)(2x-1)}-\frac{(2x+1)(2x+1)}{(2x-1)(2x+1)}-\frac{4}{1-4x^2}=0$

Запишем их в одну общую дробь.

$\frac{(2x-1)(2x-1)-(2x+1)(2x+1)}{(2x+1)(2x-1)}-\frac{4}{1-4x^2}=0$

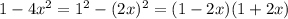
Заметим, что в знаменателе вычитаемого тоже есть формула разности квадратов, т.е. 1-4x^2=1^2-(2x)^2=(1-2x)(1+2x)

В уменьшаемом раскроем скобки в числителе с формул квадрата разности и квадрата суммы:

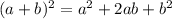
1) $(a+b)^2=a^2+2ab+b^2\\$

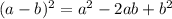
2) (a-b)^2=a^2-2ab+b^2

$\frac{(4x^2-2*2x+1)-(4x^2+2*2x+1)}{(2x+1)(2x-1)}-\frac{4}{(1-2x)(1+2x)}=0$

Раскроем скобки в числителе первой дроби еще раз и упростим получившееся выражение.

$\frac{4x^2-4x+1-4x^2-4x-1}{(2x+1)(2x-1)}-\frac{4}{(1-2x)(1+2x)}=0$ $\frac{0}{(2x+1)(2x-1)}-\frac{4}{(1-2x)(1+2x)}=0$

Теперь перенесем вычитаемое в правую часть и решим уравнение пропорцией.

$\frac{0}{(2x+1)(2x-1)}=\frac{4}{(1-2x)(1+2x)}0(1-2x)(1+2x)=(2x+1)(2x-1)*4\\(2x+1)(2x-1)*4=0\\(2x+1)(2x-1)=0:4\\(2x+1)(2x-1)=0\\\left \{ {{2x+1=0} \atop {2x-1=0}} \right. = \left \{ {{2x=-1} \atop {2x=1}} \right.=\left \{ {{x=-0,5} \atop {x=0,5}} \right.$ (в последней строке скобки должна быть не {, а [, редактор не позволяет их поставить, к сожалению)

Оба корня не подходят по ОДЗ => решений нет, ∈∅