обчисліть площу бідної поверхні прямої призи в основі якої лежить роб з діагоналями 4 і 2√5см а менша діагональ призи нахилена до призми до площини під кутом 45
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, , но сейчас это не нужно), нам повезло, это 32
Учитываем, что , получаем
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
Остаток 21, чудесно. Выполняем последний шаг.
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
По первому заданию предлагаю другие решения. Первый для тех, кто знает только проценты и пропорцию. Пусть оба шкафа сначала стоили одинаково - 100 рублей Первый шкаф подорожал на 20%. 100% --- 100 руб 20% --- х руб х = 20%*100 руб/100% = 20 руб. Новая цена первого шкафа 100+20 = 120 руб. Первый шкаф подешевел на 10% 100% --- 120 руб. 10% х руб. х = 10% * 120 руб/100% = 12 руб. Новая цена первого шкафа 120-12 = 108 руб
Второй шкаф подешевел на 10% 100% --- 100 руб 10% х руб х = 10% * 100 руб/100% = 10 руб Новая цена второго шкафа 100 - 10 = 90 руб Второй шкаф подорожал на 20% 100% 90 руб 20% х руб х = 20% * 90 руб/100% = 18 руб. Новая цена второго шкафа 90 + 18 = 108 руб.
ответ: цена будет одинаковой Второй вариант в принципе требует знание только процентов и внимательности и рассуждений. Можно решить гораздо проще и быстрее и в более общем виде: Пусть начальная цена шкафов х руб. Тогда для цены первого шкафа повышение на 20% и снижение на 10% равносильны умножению: х * 1,20 * 0,9 Объяснение. Почему умножаем на 1,20? Дело в том, что если что-то повысилось на 20%, то теперь оно составляет (100% + 20%) = 120%. А 120% - это 120 сотых, или 120/100, или 1,20. А почему умножаем на 0,9? Если что-то снизилось на 10%, то оно теперь составляет (100% - 10%) = 90%. А 90% - это 90 сотых, или 90/100, или 0,9. Для второго шкафа снижение на 10% и повышение на 20% равносильны умножению: х * 0,9 * 1,20 Как видим, оба произведения отличаются только порядком множителей, значит, они равны: х * 1,2 * 0,9 = х * 0,9 * 1,2 (Как Вы помните, 1,20 = 1,2) И равны они 1,08х Значит, исходная цена х выросла в 1,08 раз или на 8% (Мы уже знаем, что умножение на 1,08 - это повышение на 8%. 100%+8% = 108% = 108/100 = 1,08) Поэтому при начальной цене, например, 100 рублей (х=100) получаем новую цену 108 руб. (1,08х), повышение цены - на 8 рублей.
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,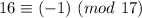 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что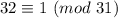 , получаем
, получаем
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
Остаток 21, чудесно. Выполняем последний шаг.
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Первый для тех, кто знает только проценты и пропорцию.
Пусть оба шкафа сначала стоили одинаково - 100 рублей
Первый шкаф подорожал на 20%.
100% --- 100 руб
20% --- х руб
х = 20%*100 руб/100% = 20 руб.
Новая цена первого шкафа 100+20 = 120 руб.
Первый шкаф подешевел на 10%
100% --- 120 руб.
10% х руб.
х = 10% * 120 руб/100% = 12 руб.
Новая цена первого шкафа 120-12 = 108 руб
Второй шкаф подешевел на 10%
100% --- 100 руб
10% х руб
х = 10% * 100 руб/100% = 10 руб
Новая цена второго шкафа 100 - 10 = 90 руб
Второй шкаф подорожал на 20%
100% 90 руб
20% х руб
х = 20% * 90 руб/100% = 18 руб.
Новая цена второго шкафа 90 + 18 = 108 руб.
ответ: цена будет одинаковой
Второй вариант в принципе требует знание только процентов и внимательности и рассуждений.
Можно решить гораздо проще и быстрее и в более общем виде:
Пусть начальная цена шкафов х руб.
Тогда для цены первого шкафа повышение на 20% и снижение на 10% равносильны умножению:
х * 1,20 * 0,9
Объяснение. Почему умножаем на 1,20? Дело в том, что если что-то повысилось на 20%, то теперь оно составляет (100% + 20%) = 120%. А 120% - это 120 сотых, или 120/100, или 1,20. А почему умножаем на 0,9? Если что-то снизилось на 10%, то оно теперь составляет (100% - 10%) = 90%. А 90% - это 90 сотых, или 90/100, или 0,9.
Для второго шкафа снижение на 10% и повышение на 20% равносильны умножению:
х * 0,9 * 1,20
Как видим, оба произведения отличаются только порядком множителей, значит, они равны:
х * 1,2 * 0,9 = х * 0,9 * 1,2 (Как Вы помните, 1,20 = 1,2)
И равны они 1,08х
Значит, исходная цена х выросла в 1,08 раз или на 8% (Мы уже знаем, что умножение на 1,08 - это повышение на 8%. 100%+8% = 108% = 108/100 = 1,08)
Поэтому при начальной цене, например, 100 рублей (х=100) получаем новую цену 108 руб. (1,08х), повышение цены - на 8 рублей.