Пусть скорость автомобиля равна , а скорость автобусов .
Первое событие: «Через 2 часа первый автобус с автомобилем встретились».
Если тела движутся навстречу друг другу, То их скорости складываются:
Второе событие: автомобиль догнал автобус через 2+5=7 часов.
Если транспортное средство едет вдогонку, то от его скорости отнимается скорость «убегающего»:
(В правой части выражения — 280 км + то расстояние, которое успел проехать автобус за 7 часов)
Объединим уравнения первого и второго событий в систему:
Отнимем от первого уравнения второе:
ответ: км/ч.
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t) - объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение:
9t = 1
Значит, - цис./ч - производительность "медленного" насоса.
Тогда - цис./ч - производительность "быстрого" насоса.
Следовательно, ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.
Пусть скорость автомобиля равна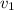 , а скорость автобусов
, а скорость автобусов 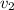 .
.
Первое событие: «Через 2 часа первый автобус с автомобилем встретились».
Если тела движутся навстречу друг другу, То их скорости складываются:
Второе событие: автомобиль догнал автобус через 2+5=7 часов.
Если транспортное средство едет вдогонку, то от его скорости отнимается скорость «убегающего»:
(В правой части выражения — 280 км + то расстояние, которое успел проехать автобус за 7 часов)
Объединим уравнения первого и второго событий в систему:
Отнимем от первого уравнения второе:
ответ: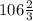 км/ч.
км/ч.
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t) - объем работы системы из двух насосов за 2ч 15мин.
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение:
9t = 1
Значит,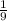 - цис./ч - производительность "медленного" насоса.
- цис./ч - производительность "медленного" насоса.
Тогда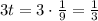 - цис./ч - производительность "быстрого" насоса.
- цис./ч - производительность "быстрого" насоса.
Следовательно,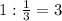 ч - потребуется "быстрому" насосу на заполнение цистерны.
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.