Нужно, 30 ! #1. найдите наименьшие целое число, являющееся решением неравенства: (х-8)^3+24х^2> =х^2+64х. #2. докажите тождество: (х^3-9у^4)^2-(х^3+9у^4)^2+36х^3(у4-х)=-36.

(см. объяснение)

Объяснение:

Введем функцию .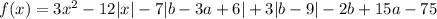

Заметим, что перед нами уравнение двух парабол, склеивающихся в фиксированной точке .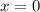

Этот график может ездить только вверх-вниз в зависимости от значений параметров и .

Уравнение может иметь ровно два корня при любом значении параметра только, если .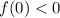

Тогда перейдем к неравенству:

Построим его в координатах .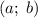

(см. прикрепленный файл)

Получили, что при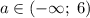 исходное уравнение имеет ровно два различных корня при любом значении параметра .

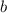ответим теперь на вопрос задачи: ниже .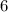

Задание выполнено!

При умножении любого числа на 0 мы получаем 0 !     !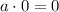

Поэтому, если задано уравнение, где в левой части стоит произведение каких-то выражений, а в правой части записан 0, то его очень легко решать, так как произведение равно нулю, когда какой-либо из множителей равен 0.

(х-4)(х-5)(х-6)=0  , если либо (х-4)=0, либо  (х-5)=0 , либо  (х-6)=0 .

То есть либо х=4 , либо х=5 , либо х=6 .

Значит мы получили три значения переменной "х", при которых левая часть обратиться в 0 . Это и есть корни уравнения.

Проверим, подставим вместо "х" значение 4, получим  

(4-4)(4-5)(4-6)=0*(-1)*(-2)=0 .

х=5:  (4-5)(5-5)(5-6)=(-1)*0*(-1)=0 ,

х=6:  (6-4)(6-5)(6-6)=2*1*0=0 .

ответ:  х₁=4 , х₂=5 , х₃=6 .