Нужна не могу найти ошибку или я неправильно решил. =( в прямоугольном треугольнике abc с прямым углом c, тангенс внешнего угла при вершине a равен −3√10/20 *sqrt(10))/20) , сторона bc равна 3. найдите сторону ab. найти ! должно быть 7, но tg(180-a)=*sqrt(10))/20) tg(180-a)=-tg(a) => tg(a)=(3*sqrt(10))/20 sina=bc/ab ab=bc/sina sin(a)=sqrt(1-cos^2(a)) tg^2(a)+1=1/cos^2(a) cos^2(a)=1/(tg^2(a)+1) ab=bc/(sqrt(1-(1/(tg^2(a)+ ab=3/(sqrt(1-(1/(900/400+ ab=3/(sqrt(1-(1/(1300/ ab=3/(sqrt(1-4/13)) ab=3/sqrt(9/13) ab=3/(3/sqrt(13)) ab=sqrt(13) как?
можно проще... tgA Вы нашли верно = 3V10/20
по определению тангенс ---это отношение противолежащего катета к прилежащему катету
tgA = CB/CA = 3/CA
отсюда СА = 3/tgA = 3 : 3V10/20 = 3 * 20 / 3V10 = 20/V10
по т.Пифагора AB^2 = AC^2 + BC^2
AB^2 = 20*20/10 + 3*3 = (400 + 90)/10 = 490/10 = 49
AB = 7
У меня так.
tg a = BC/AC Отсюда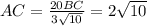
По теореме Пифагора АВ=7