No2. (3б.) решите с системы уравнений.
башни «темір жолы», называемые «голубыми китами», в нур-
султане посетили две группы туристов. они одновременно
сели на соседние лифты, решив подняться на 27 этаж. для
этого им нужно проехать 120 м. первый лифт поднялся на
нужный этаж на 0,3 мин раньше. туристы выяснили, что
скорость второго лифта на 0,5 м/с меньше скорости первого
лифта. какова скорость каждого из лифтов?
завтра сор по ​

27³ + 13³ = (27 + 13)(27² - 27*13 + 13²) = 40(27² - 27*13 + 13²) = 8*5(27² - 27*13 + 13²) делится на 8.
(2х - 5)² = 9х²
4х² - 20х + 25 = 9х²
9х² - 4х² +20х - 25 =0
5х² +20х -25 = 0
х² + 4х - 5 = 0
D больше 0, т.к. а и с имеют разные знаки. Уравнение имеет два различных корня. По обратной теореме Виета х1 + х2 = -4; х1*х2 = -5.  х1 = -5; х2 = 1.
(3а - 5)² - (2а +7)(2а - 7) = 74
9а² - 30а + 25 - 4а² +49 = 74
5а² - 30а +74 - 74 = 0
5а(а - 6) = 0
а = 0 или а - 6 = 0
                  а = 6.
ответ: 0; 6.
(х - 3)² - 12 (х - 3) + 36 = (х - 3 - 6)² = (х- 9)² = (9,3 - 9)² = 0,3² = 0,09.
(7х - 1)² - 25х² = (7х - 1 - 5х)(7х - 1 + 5х) = (2х - 1)(12х - 1) = (2*1/12 - 1)×
× (12×1/12 - 1) = -5/6×0 = 0.

 

а) x∈[0; 1,25]

б) x∈(-∞; -10]∪[8; 12)∪(12; +∞)

Объяснение:

а)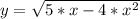

Область определения функции:

подкоренное выражение должен быть неотрицательным

5·x-4·x²≥0

x·(5-4·x)≥0

Нули левой части неравенства

х=0 и 5-4·x=0 или х=0 и x=5/4=1,25

Применим метод интервалов

x·(5-4·x):                   -                           +                                    -

       -∞      ----------- -1 -----------[0]------- 1 ----------[1,25]---------- 100 --------------> +∞

То есть  

при х= -1 : -1·(5-4·(-1)) = -1·(5+4) = -1·9 = -9<0

при х= 1 : 1·(5-4·1) = 1·(5-4) = 1·1 =1>0

при х= 100 : 100·(5-4·100)) = 100·(5-400) = 100·(-395) =-39500<0

ответ: x∈[0; 1,25]

б)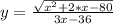

Область определения функции:

1) подкоренное выражение должен быть неотрицательным

x² + 2·x - 80≥0

Левую часть разложим на множители, для этого решаем как квадратное уравнение

D= 2²-4·1·(-80)=4+320=324=18²

x₁=(-2-18)/2= -20/2 = -10

x₂=(-2+18)/2= 16/2 = 8

(x - (-10))·(x-8)≥0

Нули левой части неравенства - это корни квадратного уравнения.

Применим метод интервалов

(x+10)·(x-8):      +                                -                                +

  -∞ ----------- -100 -----------[-10]------- 0 ----------[8]---------- 100 -------------> +∞

То есть  

при х= -100: (-100+10)·(-100-8)) = -90·(-108) = 90·108 >0

при х= 0 : (0+10)·(-8)) = 10·(-8) = -80 <0

при х= 100 : (100+10)·(100-8)) = 110·92 >0

ответ: x∈(-∞; -10]∪[8; +∞)

2) знаменатель не должен быть нулем

3·x-36≠0 или 3·x≠36 или x≠12.

Тогда ответ: x∈(-∞; -10]∪[8; 12)∪(12; +∞)