(1) Подкоренное выражение должно быть неотрицательным.
(2) Знаменатель дроби не должен быть равен нулю.
Учитывая их, записываем следующую систему.
Для начала решим отдельно верхнее неравенство системы. Его можно решить методом интервалов, предварительно разложив на множители числитель и знаменатель.
Числитель мы разложили по формуле сокращённого умножения (разность квадратов). Для разложения знаменателя понадобится найти корни следующего уравнения:
Используя следующую формулу: , где и - корни уравнения , получаем: , здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
Решим данное неравенство методом интервалов.
Нули числителя: -3; 3.
Нули знаменателя: 2; 4.
- + - + -
----------------------------------о----------------------------------о-----------------> x
Так как знак в последней строке неравенства "больше или равно", то подходят те промежутки, где стоит знак "плюс". В нашем случае: .
Решением нижнего выражения являются и . В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
Задумали два числа. Если разность этих чисел умножить на 3, то получим число, большее суммы этих чисел на 11. Если разность задуманных чисел умножить на 2, то получим число, большее суммы этих чисел на 13.
х - первое число.
у - второе число.
Математическая модель:
3*(х - у) = (х + у) + 11
2*(х - у) = (х + у) + 13
Раскрыть скобки:
3х - 3у = х + у + 11
2х - 2у = х + у + 13
Привести подобные:
2х - 4у = 11
х - 3у = 13
Выразить х через у во втором уравнении, подставить выражение в первое уравнение и вычислить у:
Нужно взять во внимание два условия.
(1) Подкоренное выражение должно быть неотрицательным.
(2) Знаменатель дроби не должен быть равен нулю.
Учитывая их, записываем следующую систему.
Для начала решим отдельно верхнее неравенство системы. Его можно решить методом интервалов, предварительно разложив на множители числитель и знаменатель.
Числитель мы разложили по формуле сокращённого умножения (разность квадратов). Для разложения знаменателя понадобится найти корни следующего уравнения:
Используя следующую формулу: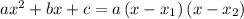 , где
, где 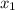 и
и 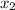 - корни уравнения
- корни уравнения 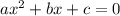 , получаем:
, получаем: 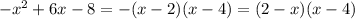 , здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
, здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
Решим данное неравенство методом интервалов.
Нули числителя: -3; 3.
Нули знаменателя: 2; 4.
- + - + -
----------------- -----------------о-----------------
-----------------о----------------- -----------------о-----------------> x
-----------------о-----------------> x
Так как знак в последней строке неравенства "больше или равно", то подходят те промежутки, где стоит знак "плюс". В нашем случае: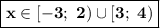 .
.
Решением нижнего выражения являются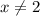 и
и 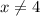 . В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
. В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
ответ: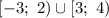 .
.
В решении.
Объяснение:
Задумали два числа. Если разность этих чисел умножить на 3, то получим число, большее суммы этих чисел на 11. Если разность задуманных чисел умножить на 2, то получим число, большее суммы этих чисел на 13.
х - первое число.
у - второе число.
Математическая модель:
3*(х - у) = (х + у) + 11
2*(х - у) = (х + у) + 13
Раскрыть скобки:
3х - 3у = х + у + 11
2х - 2у = х + у + 13
Привести подобные:
2х - 4у = 11
х - 3у = 13
Выразить х через у во втором уравнении, подставить выражение в первое уравнение и вычислить у:
х = 13 + 3у
2(13 + 3у) - 4у = 11
26 + 6у - 4у = 11
2у = 11 - 26
2у = -15
у = -7,5 - второе число.
х = 13 + 3у
х = 13 + 3*(-7,5)
х = 13 - 22,5
х = -9,5 - первое число.
Проверка:
(-9,5 + 7,5)*3 = (-9,5 - 7,5) + 11
-6 = -6, верно.
(-9,5 + 7,5)*2 = (-9,5 - 7,5) + 13
-4 = -4, верно.