Не выполняя построения, найдите ординату точки пересечения графиков функций y=4-2/7x y=9/7x+26

а) A(n) = 2 - 3 · n;  

A(1) = -1

A(2) = -4

A(3) = -7

A(4) = -10

A(5) = -13

б) A(n) = 50 - 7 · n;  

A(1) = 43

A(2) = 36

A(3) = 29  

A(4) = 22

A(5) = 15

в) B(n) = 1 ÷ n + 1;

B(1) = 2

B(2) = 1,5

B(3) =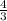  

B(4) = 1,25

B(5) = 1,2

г) B(n) = n³

B(1) = 1

B(2) = 8

B(3) = 27

B(4) = 64

B(5) = 125

Объяснение:

а) A(n) = 2 - 3 · n;  

A(1) = 2 - 3 · 1 = -1

A(2) = 2 - 3 · 2 = -4

A(3) = 2 - 3 · 3 = -7

A(4) = 2 - 3 · 4 = -10

A(5) = 2 - 3 · 5 = -13

б) A(n) = 50 - 7 · n;  

A(1) = 50 - 7 · 1 = 43

A(2) = 50 - 7 · 2 = 36

A(3) = 50 - 7 · 3 = 29  

A(4) = 50 - 7 · 4 = 22

A(5) = 50 - 7 · 5 = 15

в) B(n) = 1 ÷ n + 1;

B(1) = 1 ÷ 1 + 1 = 2

B(2) = 1 ÷ 2 + 1 = 1,5

B(3) = 1 ÷ 3 + 1 =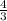

B(4) = 1 ÷ 4 + 1 = 1,25

B(5) = 1 ÷ 5 + 1 = 1,2

г) B(n) = n³

B(1) = 1³ = 1

B(2) = 2³ = 8

B(3) = 3³ = 27

B(4) = 4³ = 64

B(5) = 5³ = 125

диагонали = 10 см

Объяснение:

сумма двух разных сторон прямоугольника равна половине его периметра  14 см

Обозначим одну сторону  х

вторую  14-х

Площадь прямоугольника равна произведению его смежных сторон

составим уравнение

х(14-х)=48

14х-х^2=48

x^2-14x+48=0

найдем х через дискриминант

x1=8

x2=6

Если первая сторона равна 8 то вторая 14-х=6см

Если первая сторона равна 6 то вторая равна 14-6=8см

Стороны прямоугольника 6 см и 8 см

Теперь найдем диагональ по теореме Пифагора

пусть диагональ х

x^2= 8^2+6^2

x^2= 64+36

x^2=100

x=10  см - диагонали прямоугольника