1)
данное уравнение имеет два различных корня.
по теореме Виета:
Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.
2)
уравнение имеет два различных корня.
Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.
3)
уравнение имеет два различных корня. По т. Виета:
Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.
4)
Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.
1)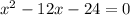
данное уравнение имеет два различных корня.
по теореме Виета:
Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.
2)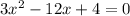
уравнение имеет два различных корня.
по теореме Виета:
Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.
3)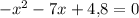
уравнение имеет два различных корня. По т. Виета:
Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.
4)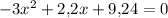
уравнение имеет два различных корня. По т. Виета:
Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.
а) 12a^2b-27b^3=3b(4a²-9b²)=3b(2a-3b)(2a+3b)
б) -40x^3-120x^2y-90xy^2=-10x(4x²+12xy+9y²)=-10x(2x+9y)²
в) 2a^4-16ab^3=2a(a³-8b³)=2a(a-2b)(a²+2ab+4b²)
г) (x^3+8)-(3x+6)=(x³+2³)-3(x+2)=(x+2)(x²-2x+4-3)=(x+2)(x²-2x+1)=(x+2)(x-1)²
2. Решите уравнение
x^3-x^2-25x+25=0
x²(x-1) - 25(x-1) = 0
(x-1)(x²-25)=0
(x-1)(x-5)(x+5)=0
x-1=0 x-5=0 x+5=0
x=1 x=5 x=-5
3. Разложите многочлен 81y^2-36xy-60x^2 на множители, выделив полный квадрат двучлена.
81y²-36xy-60x²=(9y)²-2·9y·2x+(2x)² - 64x² = (9y-2x)²-(8x)² =
= (9y-2x-8x)(9y-2x+8x)= (9y-10x)(9y+6x)