В решении.
Объяснение:
1) Укажите допустимые значения переменных в выражениях:
а/(5а + 1); (12 + х)/(8 - 8х + 2х²).
Допустимыми значениями переменных будут те, при которых дробь имеет смысл, то есть, при которых знаменатель дроби не будет равен нулю.
Приравнять знаменатель дроби к нулю и найти НЕДОПУСТИМЫЕ значения переменных, все остальные будут ДОПУСТИМЫМИ.
а) 5а + 1 = 0;
5а = -1;
а = -1/5;
а = -0,2;
Допустимы любые значения а, кроме а = -0,2.
б) 8 - 8х + 2х² = 0
2х² - 8х +8 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 64 - 64 = 0 √D=0
х₁,₂=(-b±√D)/2a
х₁,₂=(8±0)/4
х₁,₂=8/4
х₁,₂=2;
Допустимы любые значения х, кроме х = 2.
2) Упростить:
По действиям:
На фото.
y = -x
1) Функция имеет единственный ноль к точке (0, 0)
2) Область определения функции ( -∞ ; +∞)
3) Область значений такая же, т.е. ( -∞ ; +∞)
4) Область определения совпадает с областью значений
5) Функция располагается в 2 и 4 четвертях
6) Функция положительна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент отрицателен
7) Функция отрицательна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент положителен
8) Это монотонно убывающая функция
9) Функция убывает на всей своей области определения
10) Функция не имеет периода
11) График этой функции - прямая, проходящая через центр координат
12) Это нечётная функция
13) Тангенс угла наклона касательной к точке графика постоянен и равен -1 для всех х
14) Площадь под графиком от 0 до х равна
Здесь все свойства функции, выбирайте нужные.
На графике красным - сам график
Голубым подписаны четверти, их подписывать не обязательно.
В решении.
Объяснение:
1) Укажите допустимые значения переменных в выражениях:
а/(5а + 1); (12 + х)/(8 - 8х + 2х²).
Допустимыми значениями переменных будут те, при которых дробь имеет смысл, то есть, при которых знаменатель дроби не будет равен нулю.
Приравнять знаменатель дроби к нулю и найти НЕДОПУСТИМЫЕ значения переменных, все остальные будут ДОПУСТИМЫМИ.
а) 5а + 1 = 0;
5а = -1;
а = -1/5;
а = -0,2;
Допустимы любые значения а, кроме а = -0,2.
б) 8 - 8х + 2х² = 0
2х² - 8х +8 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 64 - 64 = 0 √D=0
х₁,₂=(-b±√D)/2a
х₁,₂=(8±0)/4
х₁,₂=8/4
х₁,₂=2;
Допустимы любые значения х, кроме х = 2.
2) Упростить:
По действиям:
На фото.
Объяснение:
y = -x
1) Функция имеет единственный ноль к точке (0, 0)
2) Область определения функции ( -∞ ; +∞)
3) Область значений такая же, т.е. ( -∞ ; +∞)
4) Область определения совпадает с областью значений
5) Функция располагается в 2 и 4 четвертях
6) Функция положительна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент отрицателен
7) Функция отрицательна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент положителен
8) Это монотонно убывающая функция
9) Функция убывает на всей своей области определения
10) Функция не имеет периода
11) График этой функции - прямая, проходящая через центр координат
12) Это нечётная функция
13) Тангенс угла наклона касательной к точке графика постоянен и равен -1 для всех х
14) Площадь под графиком от 0 до х равна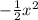
Здесь все свойства функции, выбирайте нужные.
На графике красным - сам график
Голубым подписаны четверти, их подписывать не обязательно.