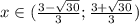Нахождение промежутков возрастания функции сводится к задаче нахождения таких значений Х, при которых производная от исходной функции будет больше 0.
Значит нам надо взять производную:
Теперь осталось решить неравенство:
найдем сначала корни уравнения:
Это была парабола ветви которой направлены вниз, потому что перед стиот отрицательный коэффициент. Значит промежуток где лежит между ее корней, значит и промежуток возрастания исходной функции лежит между ее корней.
Нахождение промежутков возрастания функции сводится к задаче нахождения таких значений Х, при которых производная от исходной функции будет больше 0.
Значит нам надо взять производную:
Теперь осталось решить неравенство:
найдем сначала корни уравнения:
Это была парабола ветви которой направлены вниз, потому что перед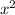 стиот отрицательный коэффициент. Значит промежуток где
стиот отрицательный коэффициент. Значит промежуток где 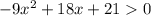 лежит между ее корней, значит и промежуток возрастания исходной функции лежит между ее корней.
лежит между ее корней, значит и промежуток возрастания исходной функции лежит между ее корней.
Таким образом: функция возрастает на интервале: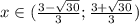
ответ: функция возрастает на интервале: