Войти
Регистрация
Спроси ai-bota
В
Все
Б
Биология
Б
Беларуская мова
У
Українська мова
А
Алгебра
Р
Русский язык
О
ОБЖ
И
История
Ф
Физика
Қ
Қазақ тiлi
О
Окружающий мир
Э
Экономика
Н
Немецкий язык
Х
Химия
П
Право
П
Психология
Д
Другие предметы
Л
Литература
Г
География
Ф
Французский язык
М
Математика
М
Музыка
А
Английский язык
М
МХК
У
Українська література
И
Информатика
О
Обществознание
Г
Геометрия
Показать больше
Показать меньше
ququqhbqha
18.04.2022 20:27 •
Алгебра
найти производную функции
Показать ответ
Ответ:
AjdanaLife
14.10.2020 04:13
Найти производную функции
и вычислить ее значение в точке x₀ = 4.
0,0
(0 оценок)
Популярные вопросы: Алгебра
kornienko123456
14.06.2020 12:51
Производительность труда мастера на 12 деталей в час больше, чем производительность труда ученика. Мастер работал 3 ч., а ученик — 6 ч. Определи количество деталей...
Ви2006ка
18.11.2021 09:29
8x - 2 ( x + 5) + ( x-1)...
haaahahaha12345
15.04.2021 20:48
если что ^ это в степени ...
sayhun
07.08.2020 16:03
Избавьтесь от иррациональности в знаменателе дроби ...
alsav241357
19.01.2023 18:09
Разложить на множители:у*2+6у+9...
Nastias1603
25.01.2020 19:12
В школе 400 учеников, 60% из них учаться на „4 и „5 . Сколько учеников учаться на „4 и „5 ....
Stesha678975425789
25.09.2022 21:42
Использовать вынесение множителя из под знака корня для доказательства следующих тождеств 1) 3√2+2-√18=2 2) √45-1-3√5=-1 3) 4√3+5-√48=5 4) √500+3-10√5=3...
feo073007feo
15.07.2020 21:11
Решите ничего не понимаю......
ivasil2012
19.12.2020 16:15
Реши уравнение 16x^2+4=0...
frhjkvg11
01.06.2023 14:17
Розв яжіть систему рівнянь алгебраїчного додавання:x+y=9;-x+y=-3....
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Найти производную функции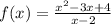 и вычислить ее значение в точке x₀ = 4.
и вычислить ее значение в точке x₀ = 4.