Но мы представим 1 как дробь , такое действие еще называют домножением на сопряжённое
3 Соберем все в одну дробь
4 Заметим в знаменателе разность квадратов
где
5 Упростим знаменатель
6 Представим дробь как произведение7 Представим предел произведения как произведение пределов8 Посчитаем первый предел9 Так как то мы можем заметить в пределе на 10 Умножим выражение пол пределом на 1
Но 1 мы представим в виде
11 Вынесем константу (3) за предел
12 Имеем первый замечательный предел, он равен 1ОТВЕТ
Но мы представим 1 как дробь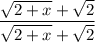 , такое действие еще называют домножением на сопряжённое
, такое действие еще называют домножением на сопряжённое
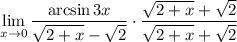
3 Соберем все в одну дробь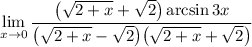
4 Заметим в знаменателе разность квадратов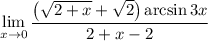
5 Упростим знаменатель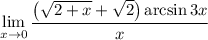
6 Представим дробь как произведениеНо 1 мы представим в виде
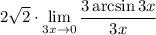
11 Вынесем константу (3) за предел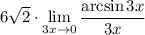
12 Имеем первый замечательный предел, он равен 1