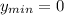На заданном нам интервале расположена только одна точка второго решения:
Т.к. наибольшее и наименьшее значение функции ищем на конечном промежутке, то необходимо проверить на экстремум и точки начала и конца промежутка:
Наибольше значение функции на заданном промежутке , а наименьшее
На заданном нам интервале расположена только одна точка второго решения:
Т.к. наибольшее и наименьшее значение функции ищем на конечном промежутке, то необходимо проверить на экстремум и точки начала и конца промежутка:
Наибольше значение функции на заданном промежутке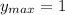 , а наименьшее
, а наименьшее