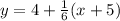Дифференциальное уравнение является уравнение с разделяющимися переменными.
Разделим переменные:
Проинтегрируем левую и правую части уравнения, получим:
Найдем теперь частное решение, подставляя начальные условия:
ЧАСТНОЕ РЕШЕНИЕ :
Дифференциальное уравнение является уравнение с разделяющимися переменными.
Разделим переменные: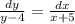
Проинтегрируем левую и правую части уравнения, получим:
Найдем теперь частное решение, подставляя начальные условия:
ЧАСТНОЕ РЕШЕНИЕ :