Найти частное решение дифференциального уравнения, удовлетворяющего указанным начальным условиям:
y=1 при x=2

Показать ответ

Ответ:

hlebushek225

10.09.2020 03:40

ответ: 35

Объяснение:

Предположим, что в классе менее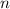 человек, причем 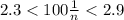2.3 ,тогда минимальный процент неуспевающих учеников будет достигнут при наибольшем возможном числе учеников, то есть n-1 и при минимальном числе неуспевающих учеников, то есть .

Таким образом, при таком условии процент неуспевающих учеников :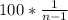 $100*\frac{1}{n-1}$

Найдем минимальное число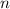 удовлетворяющее неравенству:

2.3

Предположим, что в классе менее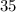 человек, тогда минимальный процент учеников неуспевающих в классе

$100\frac{1}{34} =\frac{100}{34} = 2+ \frac{32}{34} = 2+ \frac{16}{17}$

Сравним:

$2+\frac{16}{17}$ и 2.9

$2+\frac{16}{17}$ и $2+\frac{9}{10}$

$\frac{16}{17}$ и $\frac{9}{10}$

$\frac{160}{170}\frac{153}{170}$

$100\frac{1}{34} 2.9$

То есть мы пришли к противоречию. А значит в классе как минимум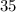 человек. C другой стороны, как было показано выше, для случая 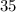человек может быть достигнут процент неуспевающих учеников в пределах от 2,3% до 2,9%. Это произойдет когда в классе из 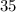человек неуспевает ровно ученик.

0,0(0 оценок)

Ответ:

wigler

16.01.2020 05:57

Объяснение:

При n=1 верность неравенства очевидна.

При n=2, получаем известное верное неравенство, оно нам понадобится.

$\frac{a+b}{2} \geq \sqrt{ab}$

Теперь докажем, что из верности неравенство верно для n=m, следует его верность для n=2m.

В самом деле, пусть неравенство верно для n=m. Нам нужно доказать, что тогда верно и неравенство

$\frac{a_1+a_2+...+a_m+a_{m+1}+...+a_{2m}}{2m} \geq \sqrt[2m]{a_1a_2...a_{2m}}$

Так как неравенство верно для n=m (по индуктивному предположению), можем записать такие два неравенства:

$\frac{a_1+a_2+...+a_m}{m} \geq \sqrt[m]{a_1a_2...a_{m}} \\\frac{a_{m+1}+a_{m+2}+...+a_{2m}}{m} \geq \sqrt[m]{a_{m+1}...a_{2m}} \\$

Теперь сложим эти неравенства и разделим обе части полученного на 2. Получится вот такое неравенство:

$\frac{a_1+a_2+...+a_{2m}}{2m} \geq \frac{\sqrt[m]{a_1a_2...a_{m}}+\sqrt[m]{a_{m+1}...a_{2m}}}{2}$

Но использовав неравенство для n=2 получаем:

$\frac{\sqrt[m]{a_1a_2...a_{m}}+\sqrt[m]{a_{m+1}...a_{2m}}}{2} \geq \sqrt{\sqrt[m]{a_1a_2...a_{m}}\sqrt[m]{a_{m+1}...a_{2m}}} =\sqrt[2m]{a_1a_2...a_{2m}}$

Тогда и подавно

$\frac{a_1+a_2+...+a_{2m}}{2m} \geq \sqrt[2m]{a_1a_2...a_{2m}}$

А теперь, следуя за Коши (который как раз первым доказал это неравенство), заметим, что из доказанного выше следует, что если неравенство верно для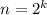 n=2^k (где k - натуральное), то оно верно и для 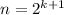$n=2^{k+1}$ . Действительно, чтобы доказать это, достаточно положить 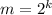m=2^k , тогда 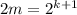$2m=2^{k+1}$ и неравенство также верно. А так как неравенство верно для n=2, то по индукции отсюда получаем верность неравенства для всех остальных степеней двойки, то есть для чисел вида 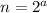n=2^a при любом натуральном . Это утверждение назовём Леммой 1.

Осталось доказать, что из верности неравенства для n=k, следует его верность для n=k-1. Это будет наша Лемма 2.

Ну что же, раз в задании дана такая превосходная подсказка - воспользуемся ей. Найдём такой x, о котором идёт речь в задании. Он выражается из данной в условии формулы очевидным образом, не буду на этом останавливаться:

$x=\frac{a_1+a_2+...+a_{n-1}}{n-1}$

Теперь пусть неравенство верно для произвольного n=k.

Применим это неравенство к числам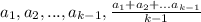 $a_1, a_2, ... , a_{k-1}, \frac{a_1+a_2+...a_{k-1}}{k-1}$ :

$\frac{a_1+...+a_{k-1}+\frac{a_1+...+a_{k-1}}{k-1} }{k} \geq \sqrt[k]{a_1...a_{k-1}\frac{a_1+...+a_{k-1}}{k-1}}$

Что получится в левой части мы знаем - среднее арифметическое чисел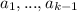 $a_1, ... , a_{k-1}$ . Далее возводим неравенство в степень k и преобразовываем:

$\bigg(\frac{a_1+...+a_{k-1}}{k-1} \bigg)^k\geq a_1...a_{k-1}\frac{a_1+...+a_{k-1}}{k-1}\\\bigg(\frac{a_1+...+a_{k-1}}{k-1} \bigg)^{k-1}\geq a_1...a_{k-1}\\\frac{a_1+...+a_{k-1}}{k-1}\geq \sqrt[k-1]{a_1...a_{k-1}}$

Получили как раз неравенство для n=k-1.

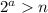Собственно, неравенство можно считать доказанным. Лемма 1 и Лемма 2 решают вопрос для любого n. В самом деле, возьмём произвольное натуральное n. Очевидно, найдётся такое натуральное , что 2^an . Неравенство верно для этой степени двойки (Лемма 1). Но оно верно также и для всех натуральных чисел меньших её, это по индукции следует из Леммы 2. Тогда неравенство верно и для нашего произвольно выбранного n.