Рассмотрим числовую последовательность в которой члены - это количество камешков в каждом уголке, т.е.
а1=1
а2=3=1+2=а1+2
а3=5=3+2=а2+2
а4=7=5+2=а3+2
Замечаем, что данные числа образуют арифметическую прогрессию с разность d=2 (каждый следующий член получен из предыдущего увеличением на одно и тоже число - 2).
По формуле n-го члена арифметической прогрессии
аn=а1+(n-1)*d
находим, что а100=1+(100-1)*2=1+99*2=1+198=199, т.е. в сотом уголке - 199 камешков.
А, теперь, используя формулу для нахождения суммы первых n членов арифметической прогрессии
1.
ОДЗ: арксинус определен при![x\in[-1;\ 1]](/tpl/images/1421/5878/61ea0.png)
Найдем синус левой и правой части:
Уравнение распадается на два. Для первого уравнения получим:
Решаем второе уравнение:
Таким образом, уравнение имеет единственный корень 0.
ответ: 0
2.
ОДЗ: арксинус определен при![x\in[-1;\ 1]](/tpl/images/1421/5878/61ea0.png)
Найдем синус левой и правой части:
Так как в правой части стоит положительная величина, то и левая часть должна быть положительной, то есть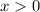 .
.
Возведем в квадрат обе части:
Решим биквадратное уравнение:
Находим х:
Однако, так как было выявлено ограничение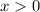 , то отрицательный корень не попадает в ответ.
, то отрицательный корень не попадает в ответ.
Оценив значение полученного корня, мы понимаем, что он удовлетворяет исходной ОДЗ:
ответ: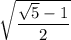
Рассмотрим числовую последовательность в которой члены - это количество камешков в каждом уголке, т.е.
а1=1
а2=3=1+2=а1+2
а3=5=3+2=а2+2
а4=7=5+2=а3+2
Замечаем, что данные числа образуют арифметическую прогрессию с разность d=2 (каждый следующий член получен из предыдущего увеличением на одно и тоже число - 2).
По формуле n-го члена арифметической прогрессии
аn=а1+(n-1)*d
находим, что а100=1+(100-1)*2=1+99*2=1+198=199, т.е. в сотом уголке - 199 камешков.
А, теперь, используя формулу для нахождения суммы первых n членов арифметической прогрессии
Sn=((a1+an)*n)/2
получаем, что в первых 100 уголках будет камешков
S100=((1+199)*100)/2=(200*100)/2=100*100=10000
ответ: 10000