Найдите уравнение прямой параллельной прямой y=2x и проходящей через точку D (1;1) y=2x+1
y=2x-1
y=2x-4
y=2x+7
y=2x-3

Выразим катет а из формулы:

домножим обе части уравнения на два (и поменяем их местами заодно):

извлечём корень квадратный из обеих частей уравнения:

При площади треугольника в 10см², длина катета будет равна:

см

Это точное значение (я его немного упростил, хотя можно было записать даже перемножив числа под корнем, получив )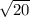

Вычислим на калькуляторе это значение, получим десятичную дробь (с кучей знаков после запятой), затем округлим её до одного знака после запятой:

см

Начертить такой треугольник (используя приближённое значение длины катета) можно, расположив катеты по клеткам тетради (как раз будет ровное число клеток).

Равнобедренный прямоугольный треугольник выглядит как половинка квадрата с такой же стороной, как катет треугольника (смотри рисунок внизу).

1. снование равно 12,8, так треугольник равнобедренный, а боковая сторона равна 8

2. По признаку о равнобедренном треугольнике, что высота проведенная из вершины угла, является и биссектрисой и медианой, так как высота это медиана, то получается что высота делит треугольник пополам.

3. Мы получили прямоугольный треугольник

По теореме Пифагора находим высоту, то есть:

а^2+в^2=с^2 (где а и в-катеты, а с-гипотенуза)

пусть в-Х,

а=1/2 основная, что равно 6,4

с-боковая сторона, что по условию равно 8

подставим числа

8^2=6,4^2+х^2

64=40,96+х^2

х^2=23,04

х=4,8