Алгебра: Найдите угол дбс, можете расписать решение

Найдите угол дбс, можете расписать решение

Показать ответ

Ответ:

настюшанастя1200

11.05.2022 17:06

Объяснение:

1. Дана функция у = 8х − 3

1)Найти значение у, для этого известное значение аргумента (х=2) подставить в уравнение и вычислить у:

у=8*2-3=13 при х=2 у=13

2)Найти значение х при известном значении у. Подставляем в уравнение значение у= -19 и вычисляем значение х:

-19=8х-3

-8х= -3+19

-8х=16

х= -2 у= -19 при х= -2

3)Чтобы определить, проходит ли график данной функции через точку В (-2; -13) нужно подставить известные значения х и у (координаты точки) в уравнение, если левая часть равна правой, проходит, и наоборот:

-13=8*(-2)-3

-13= -16-3

-13≠ -19, не проходит.

2. Постройте график функции у = −2х + 5

Уравнение линейной функции прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.

Таблица:

х -1 0 1

у 7 5 3

1)х=2, определяем значение у как в предыдущем задании:

у= -2*2+5=1 при х=2 у=1

2)у= -1, определяем значение х как в предыдущем задании:

-1= -2х+5

2х=5+1

2х=6

х=3 у= -1 при х=3

3)у= -0,3х+4

График функции пересекает ось Х при у=0, ось У при х=0.

а)х=0 у=4 точка пересечения графиком оси У.

б)у=0 0= -0,3х+4 0,3х=4 х=4/0,3=13 и 1/3 - точка пересечения графиком оси Х.

4)y=kx+8 А(-3;20) k=?

Чтобы найти k, нужно подставить известные значения х и у (координаты точки А) в уравнение и вычислить k:

20=k*(-3)+8

20= -3k+8

3k=8-20

3k= -12

k= -4

5)Неясная запись задания.

0,0(0 оценок)

Ответ:

юли10

29.01.2022 14:22

-4

Объяснение:

Такие задачи решаем по схеме:

1. Найти производную функции.

2. Найти нули производной: для этого приравнять производную к нулю и решить уравнение.

3. Построить числовую ось, отметить найденные точки и определить знаки производной на полученных интервалах.

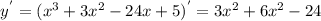
1. $y^{'} = (x^{3} + 3x^{2} - 24x + 5)^{'} =3x^{2} + 6x^{2} - 24$

$3x^{2} + 6x^{2} - 24 = 0 \\3(x^{2} + 2x^{2} - 8) = 0\\D = 2^{2} 4 - 4*(-8)*1 = 4 + 32 = 36\\x_{1} = \frac{-2 + \sqrt{36} }{2} = \frac{-2 + 6 }{2} = 2\\x_{2} = \frac{-2 - \sqrt{36} }{2} = \frac{-2 - 6 }{2} = -4$

3. На рисунке.

Как определены знаки на интервалах: берем произвольную точку из одного из интервалов, например на среднем, который от -4 до 2. На этом интервале лежит, например число 0. его и возьмем. Подставим в производную:

$y^{'} =3x^{2} + 6x^{2} - 24\\y^{'}(0) = 3*0^{2} + 6*0 - 24 = 0 + 0 - 24 = -24$