Найдите такое значение t, при котором многочлен стандартного вида, торжественно равный произведению (x²+2x+3)(x-t), не содержит x².
t=?

Показать ответ

Ответ:

витя55346

05.01.2021 08:43

Объем работы (заказ) = 1 (целая)
1) 3 ч. 36 мин. = 3 ³⁶/₆₀ ч. = 3,6 часа
1 : 3,6 = 1 *  ¹⁰/₃₆ = 1 * ⁵/₁₂ =  ⁵/₁₂ (частей) объема работы в час выполняют два рабочих при совместной работе
2) 1 : 6 = ¹/₆ (часть) объема работы в час выполняет
I рабочий самостоятельно
3) ⁵/₁₂ - ¹/₆ = ⁵/₁₂ -  ²/₁₂ = ³/₁₂ = ¹/₄ (часть) объема работы в час выполняет II рабочий самостоятельно
4) 1 :  ¹/₄ = 1 *  ⁴/₁ = 4 (часа)

ответ : 4 часа необходимо второму рабочему для выполнения заказа, если он будет работать один.

0,0(0 оценок)

Ответ:

sanya1897p08pyj

14.03.2020 09:33

$\frac{1 + \sqrt{x} + x}{1 + \sqrt{x} } = \frac{1 + \sqrt{x} + x }{1 + \sqrt{x} } \times \frac{1 - \sqrt{x} }{1 - \sqrt{x} } = \frac{(1 + \sqrt{x} + x)(1 - \sqrt{x}) }{(1 + \sqrt{x} )(1 - \sqrt{x}) } = \frac{ {1}^{3} - {( \sqrt{x} )}^{3} }{1 - x} = \frac{1 - x \sqrt{x} }{1 - x}$

Пояснение:

Выражения такого типа, когда в знаменателе сумма или разность числа и числа под корнем, избавляются от иррациональности простым методом. Вспоминаем формулу сокращенного умножения, разность квадратов:

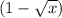${a}^{2} - {b}^{2} = (a - b)(a + b)$ . В нашем примере в знаменателе сумма, то есть (a + b) из формулы. Нам нужно найти (a - b) и умножить на это дробь, чтобы потом получилось ${a}^{2} - {b}^{2}$ , а ${( \sqrt{x} )}^{2} = x$ , получится просто число, таким образом избавимся от корня в знаменателе. В нашем случае — это , — это $\sqrt{x}$ . Соответственно, (a - b) — это $(1 - \sqrt{x} )$ .

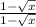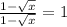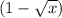Важно отметить, что нужно умножить наше выражение не просто на $(1 - \sqrt{x} )$ , а на $\frac{1 - \sqrt{x} }{1 - \sqrt{x} }$ , потому что $\frac{1 - \sqrt{x} }{1 - \sqrt{x} } = 1$ , а при умножении на 1 значение выражения не измениться. Если умножить просто на $(1 - \sqrt{x} )$ значение выражения поменяется.