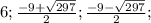графики функций y1=(a−6)x2−1 и y2=2ax+8 имеют одну общую точку, если уравнение
имеет одно единственное решение
(*)
Если а=6 то уравнение линейное и имеет вид
-12x-9=0
x=9/(-12)=-0.75 - одно решение
Если а не равно 6, тогда уравнение (*) квадратное и имеет одно решение в случае если дискриминант равен 0, т.е.
D=(-2a)^2-4*(a-6)*(-9)=0
4a^2+36(a-6)=0;
a^2+9(a-6)=0;
a^2+9a-54=0;
D=9^2-4*1*(-54)=297
ответ:
графики функций y1=(a−6)x2−1 и y2=2ax+8 имеют одну общую точку, если уравнение
имеет одно единственное решение
Если а=6 то уравнение линейное и имеет вид
-12x-9=0
x=9/(-12)=-0.75 - одно решение
Если а не равно 6, тогда уравнение (*) квадратное и имеет одно решение в случае если дискриминант равен 0, т.е.
D=(-2a)^2-4*(a-6)*(-9)=0
4a^2+36(a-6)=0;
a^2+9(a-6)=0;
a^2+9a-54=0;
D=9^2-4*1*(-54)=297
ответ: