Найдите расстояние между точками m(-3;7) n(3;-1).

Существует несколько вычисления квадратного корня числа вручную. Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители. Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.

Объяснение:

1. а)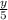 ∈{-2,-1} ⇒ y∈{-10,-5} (условие выполняется)

б)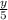 ∈{0}, тогда 0<1, но 0<3 ⇒ противоречие  

в)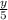 ∈{-5, -1}, y∈{-10,-5}

г)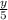 ∈{15}, y∈{75}, но y<5 ⇒ противоречие

2. a∈{5,6,7,8,9,10,11,12,13,14,15,16}, b∈{9,10,11,12}

a) a∈{5,6,7,8,9,10,11,12,13,14,15,16}, b∈{9,10,11,12}

б) a∈{5,6,7}, b∈{9,10,11,}, a+b∈{14,15,16}

в) a∈{5,6,7,8,9,10,11,12,13,14,15,16}, b∈{9,10,11,12} a+b∈{14,15,16,17,18}  

3. A) a>0

б) a < 0

в) a-8 (всегда) < a + 8 ⇒ противоречие

г) при возведение в квадрат любого числа получится положительное ⇒ когда мы поменяем его на отрицательный после возведения, полученное значение будет < 0. Но при возведение 0^2 = 0 ⇒ a=3 единственное решение.

4. p ∈ {10, 11, 12, 13}

а) если p ∈ {10, 11, 12, 13}(по условию), то выполняется только одно из условий ⇒ противоречие

б) p ∈ {10, 11, 12, 13}

в) значение всех трех дробей должно быть отрицательным чтобы соблюдалось условие, но так как >0 приходим у противоречию

г) аналогично в

5. а), в)

6. x - а), в), г)

y - б)