Первое неравенство приравняем к нулю и решим квадратное уравнение:
х²-5х+6=0
х₁,₂=(5±√25-24)/2
х₁,₂=(5±√1)/2
х₁,₂=(5±1)/2
х₁=4/2
х₁=2
х₂=6/2
х₂=3
Начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= 2 и х=3. По графику ясно видно, что у>=0 слева и справа от значений х, то есть, решения неравенства находятся в интервале х∈ (-∞, 2]∪[3, +∞).
Неравенство нестрогое, значения х=2 и х=3 входят в число решений неравенства, поэтому скобка квадратная.
Второе неравенство также приравняем к нулю и решим квадратное уравнение:
5x²-3x-2=0
х₁,₂=(3±√9+40)/10
х₁,₂=(3±√49)/10
х₁,₂=(3±7)/10
х₁= -4/10
х₁= -0,4
х₂=10/10
х₂=1
Также начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -0,4 и х=1. Данное уравнение <0, поэтому решения неравенства находится в интервале х∈(-0,4, 1).
Неравенство строгое, скобки круглые.
На числовой оси нужно отметить оба интервала и найти пересечение решений, которое подходит двум неравенствам.
1. Простым языком: мода - то число, которое встречается чаще, медиана - это то числа, справа и слева от которого находится равное кол-во чисел.
Моды в данном случае две: 1) 6; 2) 8, т.к. эти числа встречаются в выборке чаще других.
Медиану легко найти, заметив, что всего чисел 9. Т.е. медианой будет число, стоящее на 5 месте в выборке, т.к. оно делит ее на две равные половины: справа от 5 элемента будет 4 числа и слева от него будет 4 числа. На 5 месте стоит число 8 - это и есть медиана.
Среднее значение ищем как среднее арифметическое - складываем все числа и делим на их количество:
2. Всего карточек - 15. Вероятность будем искать, воспользовавшись классическим определением вероятности: вероятность равна отношению числа благоприятных исходов к общему числу исходов: . Заметим, что во всех случаях, очевидно, .
1) Выбираем из 15 первых натуральных чисел те, что кратны 4: это числа 4, 8 и 12, т.е. таких чисел 3. Т.е. . Тогда (20%)
2) Выбираем из 15 первых натуральных чисел те, которые не кратны ни числу 3, ни числу 5: это числа 1, 2, 4, 7, 8, 11, 13, 14, т.е. таких чисел 8. Т.е. . Тогда .
ОТВЕТ: 1) 0,2; 2) .
3. Пусть в коробке черных шариков. Общее число шаров равно .
Вероятность того, что выбранный шарик - черный, согласно классическому определению вероятности, равна .
х∈(-0,4, 1).
Это и есть решение системы неравенств.
Объяснение:
Решить систему неравенств:
х²-5х+6>=0
5x²-3x-2<0
Первое неравенство приравняем к нулю и решим квадратное уравнение:
х²-5х+6=0
х₁,₂=(5±√25-24)/2
х₁,₂=(5±√1)/2
х₁,₂=(5±1)/2
х₁=4/2
х₁=2
х₂=6/2
х₂=3
Начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= 2 и х=3. По графику ясно видно, что у>=0 слева и справа от значений х, то есть, решения неравенства находятся в интервале х∈ (-∞, 2]∪[3, +∞).
Неравенство нестрогое, значения х=2 и х=3 входят в число решений неравенства, поэтому скобка квадратная.
Второе неравенство также приравняем к нулю и решим квадратное уравнение:
5x²-3x-2=0
х₁,₂=(3±√9+40)/10
х₁,₂=(3±√49)/10
х₁,₂=(3±7)/10
х₁= -4/10
х₁= -0,4
х₂=10/10
х₂=1
Также начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -0,4 и х=1. Данное уравнение <0, поэтому решения неравенства находится в интервале х∈(-0,4, 1).
Неравенство строгое, скобки круглые.
На числовой оси нужно отметить оба интервала и найти пересечение решений, которое подходит двум неравенствам.
Пересечение решений х∈(-0,4, 1).
Это и есть решение системы неравенств.
1. Простым языком: мода - то число, которое встречается чаще, медиана - это то числа, справа и слева от которого находится равное кол-во чисел.
Моды в данном случае две: 1) 6; 2) 8, т.к. эти числа встречаются в выборке чаще других.
Медиану легко найти, заметив, что всего чисел 9. Т.е. медианой будет число, стоящее на 5 месте в выборке, т.к. оно делит ее на две равные половины: справа от 5 элемента будет 4 числа и слева от него будет 4 числа. На 5 месте стоит число 8 - это и есть медиана.
Среднее значение ищем как среднее арифметическое - складываем все числа и делим на их количество: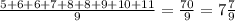
ОТВЕТ: мода - 6; 8. Медиана - 8. Среднее значение -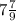
.
2. Всего карточек - 15. Вероятность будем искать, воспользовавшись классическим определением вероятности: вероятность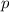
равна отношению числа 
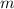благоприятных исходов к общему числу 
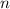исходов: 
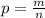. Заметим, что во всех случаях, очевидно, 
.
1) Выбираем из 15 первых натуральных чисел те, что кратны 4: это числа 4, 8 и 12, т.е. таких чисел 3. Т.е.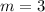
. Тогда 
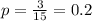(20%)
2) Выбираем из 15 первых натуральных чисел те, которые не кратны ни числу 3, ни числу 5: это числа 1, 2, 4, 7, 8, 11, 13, 14, т.е. таких чисел 8. Т.е.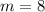
. Тогда 
.
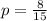ОТВЕТ: 1) 0,2; 2)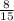
.
3. Пусть в коробке
черных шариков. Общее число шаров равно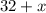 
.
Вероятность того, что выбранный шарик - черный, согласно классическому определению вероятности, равна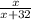
.
По условию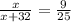
.
Решаем уравнение; по свойству пропорции:
Т.е. всего было 18 черных шаров.
ОТВЕТ: 18.