cos^2a + sin^2a = 1
соответственно:
cos^2a = 1 - (-2/3)^2
cos^2a =
cos a = +- / 3
Объяснение:
По основному тригонометрическому тождеству
sin^2 a + cos^2 a = 1
cos^2 a = 1 - sin^2 a = 1 - (-2/3)^2 = 1 - 4/9 = 5/9
cos a1 = √(5/9) = √5/3, если угол лежит в 4 четверти, 3Π/2 < a < 2Π
cos a2 = -√(5/9) = -√5/3, если угол лежит в 3 четверти, Π < a < 3Π/2
Если известно sinα, то cosα легко находим с основного тригонометрического тождества
sin²α + cos²α ≡ 1.
Отсюда, так как sinα = -2/3, то
cos²α = 1 - sin²α = 1 - (-2/3)² = 1 - 4/9 = 5/9.
Тогда
Далее, sinα<0, то π < α < 2·π. Тогда, если
π < α < 3·π/2, где косинус отрицательный, то
3·π/2 < α < 2·π, где косинус положительный, то
cos^2a + sin^2a = 1
соответственно:
cos^2a = 1 - (-2/3)^2
cos^2a =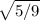
cos a = +-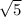 / 3
/ 3
Объяснение:
Объяснение:
По основному тригонометрическому тождеству
sin^2 a + cos^2 a = 1
cos^2 a = 1 - sin^2 a = 1 - (-2/3)^2 = 1 - 4/9 = 5/9
cos a1 = √(5/9) = √5/3, если угол лежит в 4 четверти, 3Π/2 < a < 2Π
cos a2 = -√(5/9) = -√5/3, если угол лежит в 3 четверти, Π < a < 3Π/2
Объяснение:
Если известно sinα, то cosα легко находим с основного тригонометрического тождества
sin²α + cos²α ≡ 1.
Отсюда, так как sinα = -2/3, то
cos²α = 1 - sin²α = 1 - (-2/3)² = 1 - 4/9 = 5/9.
Тогда
Далее, sinα<0, то π < α < 2·π. Тогда, если
π < α < 3·π/2, где косинус отрицательный, то
3·π/2 < α < 2·π, где косинус положительный, то