Найдите количество решений уравнения в зависимости от значений параметра `a` ({x}- дробная часть числа `a`): a+{x}=sqrt(2x-x^2). с графиком и подробным объяснением
Задание врагу не пожелаешь) Не приведи господь его на экзамене.
Что такое вообще дробная часть числа ? Это кусочно-разрывная функция. Множество её значений лежит от 0 до 1, причем так: . И состоит она из кусков прямых , при этом . (Имею в виду, что эти прямые (их бесконечно много) по факту находятся на расстоянии 1 друг от друга, но все отрезаются по просто). При этом прямая снизу обрывается при , но без разрыва, а при - сверху и с разрывом, то есть у графика будет бесконечное число выколотых точек вида , .
С этим более-менее разобрались, идем дальше. - описанная выше функция просто переносится по оси OY на единиц (при вверх, при вниз).
Теперь по правой части. Тут попроще.
Пусть у нас
Возведем в квадрат, да поделаем кое-что:
А это ни что иное, как уравнение окружности с центром в радиусом 1. Но так как у нас в условии корень, да с "+", то это верхняя полуокружность.
А теперь начинается самое веселье. Построим график полуокружности и начнем исследовать положение нашей кусочно-разрывной функции относительно этой полуокружности. Сразу отметим, что все, что находится в левой полуплоскости (левее ОY), нам не нужно (это видно по графику полуокружности), поэтому исследуем только правые "кусочки".
Будем исследовать каждый кусочек отдельно, при этом уже третий кусочек нам нужен только в случае , там будет 1 пересечение (1 корень), в остальных случаях пересечений не будет.
Исследуем второй кусочек:
При видно, что пересечений точно нет, при крайняя точка - как раз точка "разрыва", поэтому пересечений не будет, далее будет 1 пересечение, пока левая граница "кусочка" не выйдет из-за полуокружности, это будет при , при этом в нем нет разрыва, поэтому при пересечение ещё будет, поэтому имеем:
при 0 корней, при - 1 корень
Теперь исследуем первый кусочек, он самый неприятный. Видно, что прямая может иметь с частью полуокружности 0,1 или 2 общие точки. При точек будет 1, потому что это только на левом конце прямой, на правом там разрыв.
Далее до некоторого будет 2 точки пересечения, при (это значения параметра, при котором первый кусочек будет касаться полуокружности) будет 1 точка пересечения, при будет 0 точек пересечения. Найдем это
Так как касательных к окружности может быть две, но одна из них к нижней части полуокружности, которой у нас вообще нет, то остается лишь 1 касательная, которую мы и ищем фактически (но когда мы найдем, их окажется 2 как раз из-за окружности, поэтому надо будет взять верхнюю, то есть у которой значение a больше, дальше увидим).
Далее вспомним, что у 1-го кусочка прямая задается как , у 2-го кусочка , у 3-его , а так как мы ищем пересечение как раз 1-го кусочка с полуокружностью, то здесь опустим как раз дробную часть и сможем нормально решить уравнение.
Сразу говорю, у нас получится квадратное уравнение, нам нужно единственное решение, это значит, что .
Вот как раз эти два значения, берем верхнее, то есть большее
Теперь как-то структурируем ответ
При решений 0.
При будет 1 решение с 2-го кусочка.
При будет 1 решение с 1-го кусочка, 1 решение со 2-го и 1 решение с 3-его,то есть 3 решения.
При будет 2 решения с 1-го кусочка и 1 решение с 1-го кусочка, то есть 3 решения.
При будет 1 решение с 1-его кусочка и 1 решение со 2-го, то есть 2 решения.
При будет только 1 решение со 2-го кусочка
При будет 0 решений.
Объединяя все сказанное, получаем, что:
при 0 решений,
при 1 решение,
при 2 решения,
при 3 решения
P.S. К сожалению, наделать миллион графиков не так просто, функция уж больно необычная, особенно для параметра) Надеюсь, что решение более-менее понятно
Задание врагу не пожелаешь) Не приведи господь его на экзамене.
Что такое вообще дробная часть числа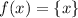 ? Это кусочно-разрывная функция. Множество её значений лежит от 0 до 1, причем так:
? Это кусочно-разрывная функция. Множество её значений лежит от 0 до 1, причем так: 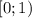 . И состоит она из кусков прямых
. И состоит она из кусков прямых 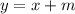 , при этом
, при этом 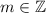 . (Имею в виду, что эти прямые (их бесконечно много) по факту находятся на расстоянии 1 друг от друга, но все отрезаются по
. (Имею в виду, что эти прямые (их бесконечно много) по факту находятся на расстоянии 1 друг от друга, но все отрезаются по 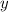 просто). При этом прямая снизу обрывается при
просто). При этом прямая снизу обрывается при 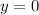 , но без разрыва, а при
, но без разрыва, а при 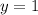 - сверху и с разрывом, то есть у графика будет бесконечное число выколотых точек вида
- сверху и с разрывом, то есть у графика будет бесконечное число выколотых точек вида 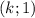 ,
, 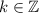 .
.
С этим более-менее разобрались, идем дальше.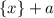 - описанная выше функция просто переносится по оси OY на
- описанная выше функция просто переносится по оси OY на 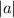 единиц (при
единиц (при 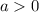 вверх, при
вверх, при 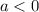 вниз).
вниз).
Теперь по правой части. Тут попроще.
Пусть у нас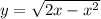
Возведем в квадрат, да поделаем кое-что:
А это ни что иное, как уравнение окружности с центром в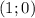 радиусом 1. Но так как у нас в условии корень, да с "+", то это верхняя полуокружность.
радиусом 1. Но так как у нас в условии корень, да с "+", то это верхняя полуокружность.
А теперь начинается самое веселье. Построим график полуокружности и начнем исследовать положение нашей кусочно-разрывной функции относительно этой полуокружности. Сразу отметим, что все, что находится в левой полуплоскости (левее ОY), нам не нужно (это видно по графику полуокружности), поэтому исследуем только правые "кусочки".
Будем исследовать каждый кусочек отдельно, при этом уже третий кусочек нам нужен только в случае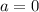 , там будет 1 пересечение (1 корень), в остальных случаях пересечений не будет.
, там будет 1 пересечение (1 корень), в остальных случаях пересечений не будет.
Исследуем второй кусочек:
При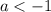 видно, что пересечений точно нет, при
видно, что пересечений точно нет, при  крайняя точка - как раз точка "разрыва", поэтому пересечений не будет, далее будет 1 пересечение, пока левая граница "кусочка" не выйдет из-за полуокружности, это будет при
крайняя точка - как раз точка "разрыва", поэтому пересечений не будет, далее будет 1 пересечение, пока левая граница "кусочка" не выйдет из-за полуокружности, это будет при 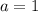 , при этом в нем нет разрыва, поэтому при
, при этом в нем нет разрыва, поэтому при 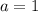 пересечение ещё будет, поэтому имеем:
пересечение ещё будет, поэтому имеем:
при![a\in (-\infty; -1] \cup (1; +\infty)](/tpl/images/1014/4203/5b0c4.png) 0 корней, при
0 корней, при ![a\in(-1;1]](/tpl/images/1014/4203/428db.png) - 1 корень
- 1 корень
Теперь исследуем первый кусочек, он самый неприятный. Видно, что прямая может иметь с частью полуокружности 0,1 или 2 общие точки. При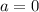 точек будет 1, потому что это только на левом конце прямой, на правом там разрыв.
точек будет 1, потому что это только на левом конце прямой, на правом там разрыв.
Далее до некоторого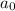 будет 2 точки пересечения, при
будет 2 точки пересечения, при 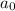 (это значения параметра, при котором первый кусочек будет касаться полуокружности) будет 1 точка пересечения, при
(это значения параметра, при котором первый кусочек будет касаться полуокружности) будет 1 точка пересечения, при  будет 0 точек пересечения. Найдем это
будет 0 точек пересечения. Найдем это 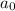
Так как касательных к окружности может быть две, но одна из них к нижней части полуокружности, которой у нас вообще нет, то остается лишь 1 касательная, которую мы и ищем фактически (но когда мы найдем, их окажется 2 как раз из-за окружности, поэтому надо будет взять верхнюю, то есть у которой значение a больше, дальше увидим).
Далее вспомним, что у 1-го кусочка прямая задается как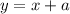 , у 2-го кусочка
, у 2-го кусочка 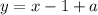 , у 3-его
, у 3-его 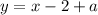 , а так как мы ищем пересечение как раз 1-го кусочка с полуокружностью, то здесь опустим как раз дробную часть и сможем нормально решить уравнение.
, а так как мы ищем пересечение как раз 1-го кусочка с полуокружностью, то здесь опустим как раз дробную часть и сможем нормально решить уравнение.
Сразу говорю, у нас получится квадратное уравнение, нам нужно единственное решение, это значит, что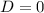 .
.
Вот как раз эти два значения, берем верхнее, то есть большее
Теперь как-то структурируем ответ
При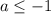 решений 0.
решений 0.
При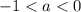 будет 1 решение с 2-го кусочка.
будет 1 решение с 2-го кусочка.
При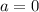 будет 1 решение с 1-го кусочка, 1 решение со 2-го и 1 решение с 3-его,то есть 3 решения.
будет 1 решение с 1-го кусочка, 1 решение со 2-го и 1 решение с 3-его,то есть 3 решения.
При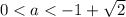 будет 2 решения с 1-го кусочка и 1 решение с 1-го кусочка, то есть 3 решения.
будет 2 решения с 1-го кусочка и 1 решение с 1-го кусочка, то есть 3 решения.
При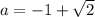 будет 1 решение с 1-его кусочка и 1 решение со 2-го, то есть 2 решения.
будет 1 решение с 1-его кусочка и 1 решение со 2-го, то есть 2 решения.
При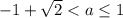 будет только 1 решение со 2-го кусочка
будет только 1 решение со 2-го кусочка
При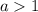 будет 0 решений.
будет 0 решений.
Объединяя все сказанное, получаем, что:
при![a \in (-\infty; -1] \cup (1; + \infty)](/tpl/images/1014/4203/fb20c.png) 0 решений,
0 решений,
при![a \in (-1;0) \cup (-1+ \sqrt{2}; 1]](/tpl/images/1014/4203/030c8.png) 1 решение,
1 решение,
при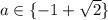 2 решения,
2 решения,
при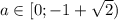 3 решения
3 решения
P.S. К сожалению, наделать миллион графиков не так просто, функция уж больно необычная, особенно для параметра) Надеюсь, что решение более-менее понятно
уж больно необычная, особенно для параметра) Надеюсь, что решение более-менее понятно