Найдите коэффициент
b
уравнения:
9
x
2
+
b
x
+
c
=
0
,
если его корнями являются числа:
2
3
и
8
3
.

Чему равно произведение корней квадратного уравнения

↓↓↓↓

Объяснение:

| x+5 | >3-x

1) {x>-5            {x>-5           {x>-5

  {x+5>3-x      {2x>-2         {x>-1         x>-1  

2) {x≤-5            {x≤-5           {x≤-5

  {-x-5>3-x      {0*x>-2         {x∈R        x≤-5

ответ x≤-5,x>-1  .

| x+5 | ≤x²+5

1) {x>-5              {x>-5           {x>-5

  {x+5≤x²+5      {х²-х≥0        {x≤0,х≥1 .         -5<x≤0  ,x≥1  

                                +         _         +

х²-х≥0 , х(х-1)≥0 , 01.

2) {x≤-5              {x≤-5                  {x≤-5

  {-x-5≤x²+5      {х²+х+10≥0        { решений нет

   х²+х+10=0 ,D<0 корней нет  

ответ       -5<x≤0  ,x≥1              

(см. объяснение)

Объяснение:

Введем функцию .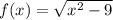

Найдем D(f):

Т.к. корень не меняет монотонность функции, то на промежутке функция 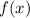убывает, а на промежутке 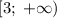возрастает.

Введем функцию .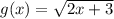

монотонно возрастает на промежутке .

Т.к. все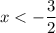  не подходят по ОДЗ для 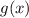, а часть функции 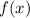, определенная на промежутке 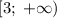, возрастает, то имеем сумму возрастающих функций, а значит возрастающая.

Значит уравнение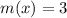 имеет единственный корень.

Предположим, что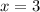 - корень уравнения.

Проверим это:

, верно.

Значит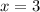 - это корень исходного уравнения.

Поэтому правильный ответ на задание 3) 3.

Уравнение решено!