Если точка Р(1;0) повернётся на угол 90° против часовой стрелки, то она перейдёт в точку с координатами Р₁(0,1). И если поворот будет по часовой стрелке, то точка будет Р₂(0,-1). Если точку Р(1;0) повернуть на 180° против часовой стрелки, то она перейдёт в точку Р₃(-1;0). Если поворот будет по часовой стрелке, то получим ту же точку Р₃(-1;0). Если точку Р(1;0) повернуть на 270° против часовой стрелки, то она перейдёт в точку Р₄(0;-1). Если поворот будет по часовой стрелке, то получим точку Р₅(0;1).
Если точку Р(1;0) повернуть на 180° против часовой стрелки, то она перейдёт в точку Р₃(-1;0). Если поворот будет по часовой стрелке, то получим ту же точку Р₃(-1;0).
Если точку Р(1;0) повернуть на 270° против часовой стрелки, то она перейдёт в точку Р₄(0;-1). Если поворот будет по часовой стрелке, то получим точку Р₅(0;1).
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение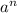
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение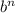
.
Рассмотрим многочлен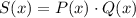
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена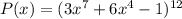
:
- степень определяется выражением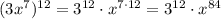
, то есть степень равна 84
- свободный член равен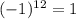
Для многочлена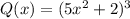
:
- степень определяется выражением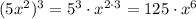
, то есть степень равна 6
- свободный член равен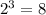
Наконец, для многочлена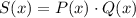
получим:
- степень определяется выражением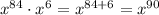
, то есть степень равна 90
- свободный член равен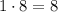
Сумма степени и свободного члена многочлена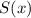
:
ответ: 98