Пусть «» кг раствора было изначально ⇒ доля соли в этом растворе ⇒ кг раствора стало после добавления соли ⇒ доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (), получим:
Домножим обе части уравнения на и , получим:
Перенесём правую часть уравнения в левую, получим:
Квадратное уравнение вида можно решить с дискриминанта .
⇒ корней будет два.
По условию концентрация соли в первоначальном растворе была меньше 20% ⇒ (массовая доля соли в первоначальном растворе) должна быть .
2
3
2x³-3x²-11x+6 |x-3
2x³-6x² 2x^2+3x-2
---------------
3x²-11x
3x²-9x
-----------------
-2x+6
-2x+6
---------------
0
x=-2 2*4+3*(-2)-2=8-6-2=0
4
15^9 оканчивается на 5
26^9 оканчивается на 6
39^9
в 1 оканчивается на 9
во 2 оканчивается на 1
в 3 оканчивается на 9
.............................................
в 9 оканчивается на 9 (в нечетной степени)
5+6+9=20,значит оканчивается на 0
5
99^9 оканчивается на 9, значит (99^99)^9 оканчивается на 9 (см 4)
6
x^4+6x³+3x²+ax+b |x²+4x+3
x^4+4x³+3x² x²+2x-8
----------------------
2x³+ +ax
2x²+8x²+6x
----------------------------
-8x²+(a-6)x+b
-8x²-32x-24
-----------------------------
0
a-6=-32⇒a=-32+6=-26
b=-24
30 кг
Объяснение:
Пусть « » кг раствора было изначально ⇒
» кг раствора было изначально ⇒ 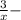 доля соли в этом растворе ⇒
доля соли в этом растворе ⇒ 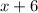 кг раствора стало после добавления соли ⇒
кг раствора стало после добавления соли ⇒ 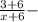 доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (
доля соли в конечном растворе. Т.к. доля соли после добавления увеличилась на 15% (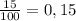 ), получим:
), получим:
Домножим обе части уравнения на и
и 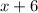 , получим:
, получим:
Перенесём правую часть уравнения в левую, получим:
Квадратное уравнение вида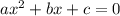 можно решить с дискриминанта
можно решить с дискриминанта 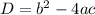 .
.
По условию концентрация соли в первоначальном растворе была меньше 20% ⇒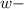 (массовая доля соли в первоначальном растворе) должна быть
(массовая доля соли в первоначальном растворе) должна быть  .
.
Значит, первоначальная масса раствора была 30 кг.