НА луче в точке О отмечены точки F и N. Найдите отpезок FN, если OF=5,6cм, ОN=3.8см. Какую длину может иметь отрезок FN

Показать ответ

Ответ:

Angelika200614

27.01.2023 13:42

(см. объяснение)

Объяснение:

(1+a^2)x^6+3a^2x^4+2(1-6a)x^3+3a^2x^2+a^2+1=0

Заметим, что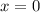 x=0 не является корнем уравнения.

Тогда поделим его на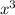 x^3 :

$(1+a^2)x^3+3a^2x+2(1-6a)+\dfrac{3a^2}{x}+\dfrac{a^2+1}{x^3}=0$

Выполним группировку:

$(1+a^2)\left(x^3+\dfrac{1}{x^3}\right)+3a^2\left(x+\dfrac{1}{x}\right)+2(1-6a)=0$

Заметим, что если - корень уравнения, то $\dfrac{1}{x}$ тоже.

Тогда единственное решение возможно, если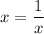 $x=\dfrac{1}{x}$ .

Иными словами, исходное уравнение может иметь ровно один корень тогда, когда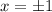 $x=\pm1$ .

Подставляя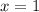 x=1 в исходное уравнение, получаем, что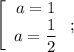 $\left[\begin{array}{c}a=1\\a=\dfrac{1}{2}\end{array}\right;$

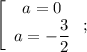
Подставляя x=-1 , получаем, что $\left[\begin{array}{c}a=0\\a=-\dfrac{3}{2}\end{array}\right;$

Теперь решим уравнение при каждом найденном значении параметра и отберем те, при которых имеется единственное решение.

Выполнив необходимые вычисления, получаем, что каждое значение параметра подходит.

Итого при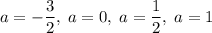 $a=-\dfrac{3}{2},\;a=0,\;a=\dfrac{1}{2},\;a=1$ исходное уравнение имеет единственное решение.

Задание выполнено!

0,0(0 оценок)

Ответ:

Lapsy

10.07.2021 09:27

$\dfrac{-\sqrt[3]{4}-\sqrt[3]{2}\pm\sqrt{2\sqrt[3]{2}+\sqrt[3]{4}+40}}{2}$

Объяснение:

x = 0 не является корнем уравнения (-729 ≠ 0). Значит, можно поделить на x³:

$x^3-33x+6+33\cdot \dfrac{9}{x}-\dfrac{729}{x^3}=0\\x^3-\dfrac{729}{x^3}-33\left(x-\dfrac{9}{x}\right)+6=0$

Пусть $x-\dfrac{9}{x}=t$ . Тогда

$t^3=x^3-3x^2\cdot\dfrac{9}{x}+3x\cdot\dfrac{81}{x^2}-\dfrac{729}{x^3}=x^3-\dfrac{729}{x^3}-27\left(x-\dfrac{9}{x}\right)\\t^3=x^3-\dfrac{729}{x^3}-27t\\x^3-\dfrac{729}{x^3}=t^3+27t$

Выполним замену:

$t^3+27t-33t+6=0\\t^3-6t+6=0$

Представим t в виде суммы двух действительных чисел: t = b + c. Заметим, что

$(b+c)^3=b^3+3b^2c+3bc^2+c^3=b^3+c^3+3bc(b+c)\\t^3=b^3+c^3+3bct\\t^3-3bct-(b^3+c^3)=0$

При подстановке t = b + c мы действительно получим 0 (чтобы убедиться в этом, достаточно проделать действия в обратном порядке), то есть t = b + c является корнем такого уравнения. Попробуем найти такие b и c, чтобы при подстановке этих чисел в последнее уравнение коэффициент перед t был равен -6, а свободный коэффициент был равен 6. Так мы получим нужное уравнение, но заодно и найдём его корень:

$\displaystyle \left \{ {{-3bc=-6} \atop {-(b^3+c^3)=6}} \right. \left \{ {{bc=2} \atop {b^3+c^3=-6}} \right. \left \{ {{c=\frac{2}{b}} \atop {b^3+\frac{8}{b^3}+6=0}} \right.$

Решим второе уравнение. b ≠ 0, иначе это противоречило бы первому уравнению (0 ≠ 2). Домножим на b³ и сделаем замену b³ = z:

z^2+6z+8=0

По теореме Виета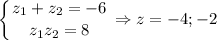 $\displaystyle \left \{ {{z_1+z_2=-6} \atop {z_1z_2=8}} \right.\Rightarrow z=-4; -2$

$\displaystyle \left [ {{b^3=-4} \atop {b^3=-2}} \right. \left [ {{b=-\sqrt[3]{4} } \atop {b=-\sqrt[3]{2} }} \right. \Rightarrow \left [ {{c=\dfrac{2}{-\sqrt[3]{4}}} \atop {c=\dfrac{2}{-\sqrt[3]{2}}} \right. \left [ {{c=-\sqrt[3]{2}} \atop {c=-\sqrt[3]{4}}} \right.$

В первом случае $t=-\sqrt[3]{4}-\sqrt[3]{2}$ , во втором — $t=-\sqrt[3]{2}-\sqrt[3]{4}$ . Они отличаются только перестановкой слагаемых, поэтому это один и тот же корень. Получаем:

$x-\dfrac{9}{x}=-\sqrt[3]{4}-\sqrt[3]{2}\\x^2+(\sqrt[3]{4}+\sqrt[3]{2})x-9=0\\D=(\sqrt[3]{4}+\sqrt[3]{2})^2+4\cdot 9=2\sqrt[3]{2}+\sqrt[3]{4}+40\\x=\dfrac{-\sqrt[3]{4}-\sqrt[3]{2}\pm\sqrt{2\sqrt[3]{2}+\sqrt[3]{4}+40}}{2}$