1. чтобы корень существовал, выражение под корнем не должно принимать отрицательных значений... 2. произведение (скобки на корень) должно получиться отрицательным (по условию), а корень четной степени не может быть отрицательным числом, потому выражение в скобке должно быть отрицательным: (-)*(+) < 0 получим систему неравенств: {x² - 1 ≤ 0 {x² - 4 ≥ 0 оба неравенства решаются методом интервалов... {(x - 1)(х + 1) ≤ 0 ---> x ∈ [-1; 1] {(x - 2)(х + 2) ≥ 0 ---> x ∈ (-∞; -2] U [2; +∞) решение системы --пересечение промежутков... ответ: {-2; 2}
выражение под корнем не должно принимать отрицательных значений...
2. произведение (скобки на корень) должно получиться отрицательным (по условию), а корень четной степени не может быть отрицательным числом, потому выражение в скобке должно быть отрицательным: (-)*(+) < 0
получим систему неравенств:
{x² - 1 ≤ 0
{x² - 4 ≥ 0
оба неравенства решаются методом интервалов...
{(x - 1)(х + 1) ≤ 0 ---> x ∈ [-1; 1]
{(x - 2)(х + 2) ≥ 0 ---> x ∈ (-∞; -2] U [2; +∞)
решение системы --пересечение промежутков...
ответ: {-2; 2}
Объяснение:
Модуль раскрывается двумя вариантами: со знаком + или со знаком - . В этой задаче 2 модуля, следовательно максимум может быть 4 раскрытия.
На практике имеем 3 области:
Область
не существует, т.к. нет пересечений у неравенств, задающих область.
Рассмотрим каждый из трех случаев:
Получили решение, лежащее в области: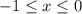
Получили неравенство, выполненное для любого x из этой области. Следовательно решение в этой области - сама область: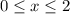
Получили решение, лежащее в области: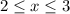
"Сшиваем" полученные решение и получаем: