Квадрат со стороной 1 см вписан во второй квадрат таким образом, что вершины первого квадрата являются серединами сторон второго. второй квадрат, аналогично, вписан в третий квадрат и т. д. получается последовательность вписанных друг в друга квадратов. а) составьте последовательность периметров полученных квадратов. выпишите первые пять членов этой последовательности . б) составьте последовательность площадей полученных квадратов. выпишите первые пять членов этой последовательности . в) чему равна длина стороны одиннадцатого квадрата? г) чему равна площадь семнадцатого квадрата?
Сторона каждого нового квадрата равна квадратному корню из суммы квадратов половинных сторон квадрата)
б) 1, 1/2, 1/4 и опять легко заметить что площади уменьшаются в 2 раза
k-коэфициент пропорциональности S1/S2=k^2=1/2
в)Фигуры подобны т.е k-коэфициент пропорциональности равен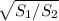 =
=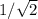 , очевидно что 11 сторона будет иметь длину
, очевидно что 11 сторона будет иметь длину
1*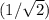 ^10 =
^10 =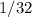
г)так как площадь нового уменьшается в 2 раза то площадь семнадцатого будет 1*(1/2)^16=1/65536