Войти
Регистрация
Спроси ai-bota
В
Все
Б
Биология
Б
Беларуская мова
У
Українська мова
А
Алгебра
Р
Русский язык
О
ОБЖ
И
История
Ф
Физика
Қ
Қазақ тiлi
О
Окружающий мир
Э
Экономика
Н
Немецкий язык
Х
Химия
П
Право
П
Психология
Д
Другие предметы
Л
Литература
Г
География
Ф
Французский язык
М
Математика
М
Музыка
А
Английский язык
М
МХК
У
Українська література
И
Информатика
О
Обществознание
Г
Геометрия
Показать больше
Показать меньше
Kisson
11.11.2022 08:22 •
Алгебра
Куб суммы и разности двух выражений. Урок 3 Найди наибольшее целое число, являющееся решением неравенства: (6 – x)3 + 2x3 > (x + 6)3 – 200x + 32. –3 –4 1 0 –2 Назад Проверить
Показать ответ
Ответ:
msnyamkina
26.02.2021 13:18
∈
Число
- это наибольшее целое число из промежутка (-∞; -2).
ответ: - 3.
0,0
(0 оценок)
Популярные вопросы: Алгебра
89115603408
21.07.2022 02:17
Сколько целых решений имеет уравнение: (1/x)+(1/y)+(1/xy)=(1/9) в скобках типо дробь...
yaach1
07.02.2021 21:08
Разложите на множители многочлен x^2+2x-9y^2+ 12y-3 только с объяснением...
strong123
09.12.2020 23:24
Найдите все корни уравнения: 27x³-54x²+36x-8=0...
VolkYula69
08.01.2020 15:34
Найдите производную f(х)=(2x-x)2-x в квадрате...
ksdaga
06.01.2022 21:08
Сколько пятизначных чисел можно составить из цифр 2,4,6,5,8 в записи каждая цифра используется только один раз ?...
TimuR2112
08.01.2023 02:08
Решите уравнение; 5х-15/(х-3)(х+2)=2/х+2...
данил20888
08.01.2023 02:08
Определите число промежутков,на которых функция принимает положительные значения f (х)=(3х^2+4)(х-1)^2(х+2)(х-3)...
Аккаунт удален
08.01.2023 02:08
Нужно решить системы с двумя переменными.один из двух подъемных кранов равной мощности может разгрузить баржу на 3 ч быстрее чем другой при совместной работе им потребовалось...
198912
30.05.2021 06:28
Варифметической прогрессии (cn): c1=4; c18=-30 найдите разность этой прогрессии...
sonia81
15.09.2020 17:33
Алгебра 8 класс Тест «Модуль числа» .1. Найдите значение выражения |х|, если х = – 2,5.А) – 2,5 и 2,5; Б) 2, 5; С) – 2,52. Вставьте вместо точек нужные по смыслу слова:...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Число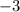 - это наибольшее целое число из промежутка (-∞; -2).
- это наибольшее целое число из промежутка (-∞; -2).
ответ: - 3.