К некоторому количеству рагу из свинины с овощами, содержащему 2 кг картофеля, добавили 3 кг картофеля, в результате чего процентное содержание свинины в рагу понизилось на 18%. Найдите первоначальную массу рагу.
Попробуем составить рекуррентное соотношение для чисел раскрасок.
Пусть для доски имеем правильных раскрасок с четным числом закрашенных клеток и правильных раскрасок с нечетным числом закрашенный клеток, для доски
: и , соответственно. Определим и для доски .
Добавим к предыдущей доске, поверх -й снизу строки, -ю строку. Вставим в нее одну из правильных раскрасок доски . У нас есть 3 варианта как мы можем закрашивать квадратики в новой строке.
Закрашиваем левую клетку, закрашиваем правую клетку или вообще не закрашиваем. Необходимо понимать, что если мы закрашиваем левую клетку в -й строке, то в -й строке закрашен правый квадратик, либо вообще ничего не закрашено и наоборот.
Пусть мы не закрасили в верхней строке ни одного квадрата, в этом случае общее число четных раскрасок : = , а нечетных :
(Будем считать, что пустая раскраска входит в число четных)
Пусть мы закрасили левый квадрат в -й строке, в этом случае либо правый квадрат -й строки закрашен, либо вообще ничего не закрашено. То есть из всех вариантов или нужно вычесть те, в которых левая клетка окрашена. Из симметрии очевидно, что числа вариантов с левой и правой окрашенной клетками равны.
Чтобы найти число всех вариантов с окрашенной левой или правой клеткой, нужно из общего числа вариантов вычесть варианты с незакрашенными клетками.
Очевидно, что число таких вариантов равно : или
Учитывая, что с добавлением одной закрашенной клетки четность меняется, то имеем:
, где и - количества правильных раскрасок с четным числом закрашенных квадратов,
с закрашенным в -й строке левым(индекс 2) и правым (индекс 3) квадратом.
Аналогично:
, где и - количества правильных раскрасок с нечетным числом закрашенных квадратов, с закрашенным в -й строке левым(индекс 2) и правым (индекс 3) квадратом.
Таким образом :
Найдем :
Когда , число вариантов с нечетным числом клеток равно (левый и правый квадрат закрашены) . С четным же числом клеток такая комбинация только одна , когда ни одна клетка не закрашена (0 клеток, 0 делится на 2).
Когда , число вариантов с нечетным числом клеток равно
(все варианты закрасить одну клетку, поскольку 3 клетки всегда будут вплотную) . С четным числом клеток имеем таких комбинаций ( две комбинации с двумя клетками по диагонали и одна комбинация с незакрашенными клетками).
Из полученного выше свойства имеем:
И так далее, то есть
Таким образом, сумма возможных значений равна:
Если вам понравилось решение, ставь лайк и отметь его лучшим.
Медиана выборки — это число, делящее пополам упорядоченную совокупность всех значений выборки по количеству, то есть половина значений выборки не большие за медиану, а половина — не меньшие. Если количество элементов нечетное (), то медианой является «среднее» число в упорядоченном их наборе, а если количество элементов четное (), то — среднее арифметическое двух «средних»чисел в этом наборе.
Например, для упорядоченной выборки, состоящей из нечетного количества элементов 3, 6, 8, 11, 19, 24, 33, медианой будет число, стоящее по середине вариационного ряда.
Например, для упорядоченной выборки, состоящей из четного количества элементов 1, 4, 4, 7, 8, 15, 24, 24, «серединой» выборки является сразу два числа: 7 и 8. Считают, что медиана такой выборки равна их среднему арифметическому: .
ответ: 0
Объяснение:
Здравствуйте!
Попробуем составить рекуррентное соотношение для чисел раскрасок.
Пусть для доски имеем
имеем 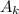 правильных раскрасок с четным числом закрашенных клеток и
правильных раскрасок с четным числом закрашенных клеток и 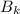 правильных раскрасок с нечетным числом закрашенный клеток, для доски
правильных раскрасок с нечетным числом закрашенный клеток, для доски
Добавим к предыдущей доске, поверх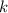 -й снизу строки,
-й снизу строки, 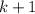 -ю строку. Вставим в нее одну из правильных раскрасок доски
-ю строку. Вставим в нее одну из правильных раскрасок доски  . У нас есть 3 варианта как мы можем закрашивать квадратики в новой строке.
. У нас есть 3 варианта как мы можем закрашивать квадратики в новой строке.
Закрашиваем левую клетку, закрашиваем правую клетку или вообще не закрашиваем. Необходимо понимать, что если мы закрашиваем левую клетку в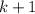 -й строке, то в
-й строке, то в 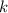 -й строке закрашен правый квадратик, либо вообще ничего не закрашено и наоборот.
-й строке закрашен правый квадратик, либо вообще ничего не закрашено и наоборот.
Пусть мы не закрасили в верхней строке ни одного квадрата, в этом случае общее число четных раскрасок :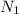 =
= 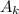 , а нечетных :
, а нечетных : 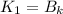
(Будем считать, что пустая раскраска входит в число четных)
Пусть мы закрасили левый квадрат в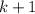 -й строке, в этом случае либо правый квадрат
-й строке, в этом случае либо правый квадрат 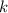 -й строки закрашен, либо вообще ничего не закрашено. То есть из всех вариантов
-й строки закрашен, либо вообще ничего не закрашено. То есть из всех вариантов 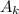 или
или 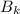 нужно вычесть те, в которых левая клетка окрашена. Из симметрии очевидно, что числа вариантов с левой и правой окрашенной клетками равны.
нужно вычесть те, в которых левая клетка окрашена. Из симметрии очевидно, что числа вариантов с левой и правой окрашенной клетками равны.
Чтобы найти число всех вариантов с окрашенной левой или правой клеткой, нужно из общего числа вариантов вычесть варианты с незакрашенными клетками.
Очевидно, что число таких вариантов равно :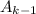 или
или 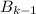
Учитывая, что с добавлением одной закрашенной клетки четность меняется, то имеем:
с закрашенным в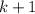 -й строке левым(индекс 2) и правым (индекс 3) квадратом.
-й строке левым(индекс 2) и правым (индекс 3) квадратом.
Аналогично:
Таким образом :
Найдем :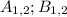
Когда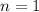 , число вариантов с нечетным числом клеток равно
, число вариантов с нечетным числом клеток равно 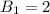 (левый и правый квадрат закрашены) . С четным же числом клеток такая комбинация только одна
(левый и правый квадрат закрашены) . С четным же числом клеток такая комбинация только одна 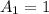 , когда ни одна клетка не закрашена (0 клеток, 0 делится на 2).
, когда ни одна клетка не закрашена (0 клеток, 0 делится на 2). 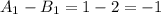
Когда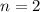 , число вариантов с нечетным числом клеток равно
, число вариантов с нечетным числом клеток равно 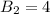
(все варианты закрасить одну клетку, поскольку 3 клетки всегда будут вплотную) . С четным числом клеток имеем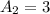 таких комбинаций ( две комбинации с двумя клетками по диагонали и одна комбинация с незакрашенными клетками).
таких комбинаций ( две комбинации с двумя клетками по диагонали и одна комбинация с незакрашенными клетками). 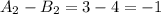
Из полученного выше свойства имеем:
И так далее, то есть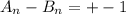
Таким образом, сумма возможных значений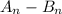 равна:
равна:
Если вам понравилось решение, ставь лайк и отметь его лучшим.
Медиана выборки — это число, делящее пополам упорядоченную совокупность всех значений выборки по количеству, то есть половина значений выборки не большие за медиану, а половина — не меньшие. Если количество элементов нечетное (
— это число, делящее пополам упорядоченную совокупность всех значений выборки по количеству, то есть половина значений выборки не большие за медиану, а половина — не меньшие. Если количество элементов нечетное (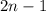 ), то медианой является «среднее» число в упорядоченном их наборе, а если количество элементов четное (
), то медианой является «среднее» число в упорядоченном их наборе, а если количество элементов четное (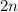 ), то — среднее арифметическое двух «средних»чисел в этом наборе.
), то — среднее арифметическое двух «средних»чисел в этом наборе.
Например, для упорядоченной выборки, состоящей из нечетного количества элементов 3, 6, 8, 11, 19, 24, 33, медианой будет число, стоящее по середине вариационного ряда.
Например, для упорядоченной выборки, состоящей из четного количества элементов 1, 4, 4, 7, 8, 15, 24, 24, «серединой» выборки является сразу два числа: 7 и 8. Считают, что медиана такой выборки равна их среднему арифметическому: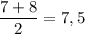 .
.