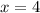Из двух городов A и B, расстояние между которыми равно 120 км, одновременно выехали две автомашины.
Скорость первой машины равна 81 км/ч, а скорость второй машины — 51 км/ч. На каком расстоянии от города B обе машины встретятся и через какое время?
1)
a) x < -5; x ∈ (-∞; -5)
б) x >= -5 ; x ∈ [-5; +∞)
в) x <= - 5 ; x ∈ (-∞; -5]
г) x > - 5; x ∈ (-5; +∞)
ответ : б)
2)
6 - положительное, целое - натуральное
3/7 - нецелое (0 < 3/7 < 1) - не натуральное
√2 - нецелое (1 < √2 < 2) - не натуральное
0 - не положительное - не натуральное
-8 - не положительное - не натуральное
-3,9 - не положительное - не натуральное
37 - положительное, целое - натуральное
п - 3,14 - положительное, целое - натуральное
-√7 - не положительное - не натуральное
ответ: 26, 37, п
3)
3√49 - 3(√2)^2
3√49 = 3*7=21
21 - 3(√2)^2
21 - 3*2 = 21 - 6 = 15
4)
5х-15<0
2x-3>=0
5x<15
2x>=3
x=3
x=3/2=1.5
x е [1.5; 3)
5) 35/3√7 * √7/√7 = 5*7*√7/3*7= 5√7/3
6)
√7×√63 - √27 ÷ √12=
=√441 - √27 ÷ √4 =
= 21 - 3÷2 =
= 39÷2 =
= 19,5
2.
Общее число партий сыгранных между англичанами и немцами, французами и немцами, англичанами и французами можно найти двумя
Пусть число французов -
Число англичан -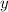
Число немцев -
Число партий вида: англичане - немцы
Число партий вида: англичане- французы
Число партий вида: немцы - французы
Таким образом :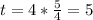
ответ: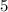
1.
Это уравнение можно переписать в виде:
Где: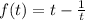
Нетрудно убедиться, что при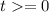
(радикалы неотрицательны) данная функция монотонно возрастет.
Действительно, ведь производная данной функции положительна.
А поскольку функция монотонна, то одинаковые значения функции могут быть только у одинаковых значений аргумента.
То есть из уравнения:
Следует равносильное ему уравнение:
ответ: