Площадь прямоугольника - , где a - длина, b - ширина прямоугольника.
Площадь квадрата - , где a - сторона квадрата.
S - площадь фигуры, всё остальное, отличное от площади фигуры, пишется с индексом рядом с буквой S
1) Чтобы найти площадь первой фигуры, нужно из общей площади сторон вычесть "вырезы"
Sобщая - bc, а выреза - . Вырезы равны, значит и площадь равная, то есть Получаем выражение , что и является ответом.
ответ:
2) Здесь из общей площади надо вычесть обрезанный кусочек, площадь которого (a-b)d, так как a-b - сторона, не данная нам, а следовательно, е' надо записать выражением. Длина нам дана - d.
Sобщая = ac
ответ:
3) Здесь единой стороны, кроме a, не дано вовсе. Чтобы найти ширину, нужно сложить m и n, так как эти числа стоят рядом и, следовательно, в сумме дают общую сторону, которая нам нужна. Но, как видим, нам ну дана противолежащая буквам m, n сторона, а для нахождения площади она является ключевой. Чтобы не усложнять себе жизнь, надо просто из а вычесть с (длина выходящего квадрата) и получить фигуру, площадь которой, при прибавлении площади вывисающего квадрата (его площадь равна по формуле выше), будет общей.
Sобщая =
Теперь, находим площадь оставшегося выреза. Это будет n(a-b-c). Теперь просто подставляем все выражения в одно единое и получаем площадь фигуры
построить график функции и описать свойства у=2(х-3)(х+1)
Точки пересечения с осью Х
х-3=0 х=3
х+1=0 х=-1 вершина лежит посредине этого отрезка.
Значит Х вершины=(3-1)/2=1 У вершины равен 2(1-3)(1+1)= -8
У этой параболы ветви вверх (поскольку х*х не имеет минуса перед собой),значит есть минимум в вершине (1;-8). Ось у пересекается в точке 2(0-3)(0+1)=6 (0;-6)
Функция убывает слева от вершины х∠1
возрастает справа от вершины 1∠х
отрицательные значения при х между точками пересечения с осью Х. (нижняя часть параболы под осью) -1∠х∠3
Положительные значения при Х правее правой и левее левой точки.
х∠-1 или 3∠х функция положительная.
график строим симметрично оси ,проходящей через вершину. имеем точку вершины (1;-8) точку на оси у (0;-6) точку на оси х.(-1;0) справа имеем точку на оси х=3 точка 0;-6 на 1 клеточку левее оси,значит такая же точка будет и справа. (2;-6) плавно соеденяешь эти точки,получаешь график.
Площадь прямоугольника -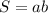 , где a - длина, b - ширина прямоугольника.
, где a - длина, b - ширина прямоугольника.
Площадь квадрата -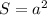 , где a - сторона квадрата.
, где a - сторона квадрата.
S - площадь фигуры, всё остальное, отличное от площади фигуры, пишется с индексом рядом с буквой S
1) Чтобы найти площадь первой фигуры, нужно из общей площади сторон вычесть "вырезы"
Sобщая - bc, а выреза -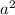 . Вырезы равны, значит и площадь равная, то есть
. Вырезы равны, значит и площадь равная, то есть 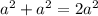 Получаем выражение
Получаем выражение 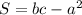 , что и является ответом.
, что и является ответом.
ответ: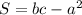
2) Здесь из общей площади надо вычесть обрезанный кусочек, площадь которого (a-b)d, так как a-b - сторона, не данная нам, а следовательно, е' надо записать выражением. Длина нам дана - d.
Sобщая = ac
ответ: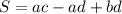
3) Здесь единой стороны, кроме a, не дано вовсе. Чтобы найти ширину, нужно сложить m и n, так как эти числа стоят рядом и, следовательно, в сумме дают общую сторону, которая нам нужна. Но, как видим, нам ну дана противолежащая буквам m, n сторона, а для нахождения площади она является ключевой. Чтобы не усложнять себе жизнь, надо просто из а вычесть с (длина выходящего квадрата) и получить фигуру, площадь которой, при прибавлении площади вывисающего квадрата (его площадь равна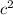 по формуле выше), будет общей.
по формуле выше), будет общей.
Sобщая =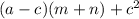
Теперь, находим площадь оставшегося выреза. Это будет n(a-b-c). Теперь просто подставляем все выражения в одно единое и получаем площадь фигуры
ответ: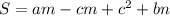
Объяснение:
построить график функции и описать свойства у=2(х-3)(х+1)
Точки пересечения с осью Х
х-3=0 х=3
х+1=0 х=-1 вершина лежит посредине этого отрезка.
Значит Х вершины=(3-1)/2=1 У вершины равен 2(1-3)(1+1)= -8
У этой параболы ветви вверх (поскольку х*х не имеет минуса перед собой),значит есть минимум в вершине (1;-8). Ось у пересекается в точке 2(0-3)(0+1)=6 (0;-6)
Функция убывает слева от вершины х∠1
возрастает справа от вершины 1∠х
отрицательные значения при х между точками пересечения с осью Х. (нижняя часть параболы под осью) -1∠х∠3
Положительные значения при Х правее правой и левее левой точки.
х∠-1 или 3∠х функция положительная.
график строим симметрично оси ,проходящей через вершину. имеем точку вершины (1;-8) точку на оси у (0;-6) точку на оси х.(-1;0) справа имеем точку на оси х=3 точка 0;-6 на 1 клеточку левее оси,значит такая же точка будет и справа. (2;-6) плавно соеденяешь эти точки,получаешь график.