I часть :
Построение графика членов арифметической прогрессии.
1) Прочитать про линейную зависимость на стр. 143-144
2) Пусть задана арифметическая прогрессия (любая), например, (аn) = 3n+1
3) Найти область определения (множество значений), область допустимых значений
4) Пометка : Каждому натуральному числу ставится в соответствии какое-то одно число (а1, а2, а3 и т.д.)
Например, а1 - 1, а2 - 2, а3 - 3
5) Лучше взять n до 5 члена арифметической прогрессии
6) Построить таблицу для графика функции
7) Построить график в прямоугольной системе координат, он будет состоять из точек, но нужно будет соединить их, чтобы показать как они расположены
8) График подписать
II часть :
1) Построение графика членов геометрической прогрессии
2) Пусть дана геометрическая прогрессия, например, (bn), b1 = 3, q = ½
3) Найти область определения, область допустимых значений
4) смотри выше, как с арифметической прогрессией в 4)
5) Написать где-нибудь после графика :
"Зависимость bn от n для членов геометрической прогрессии получила название экспоненциональной
6) Сделать таблицу для графика функции
7) Нарисовать график на прямоугольной системе координат, все точки соединить плавной линией, должна получится кривая
8) График подписать
> Чем больше график, тем лучше (например, сделать на листе А4)
> Прочитать дополнительную информацию в интернете о том, как строить такие графики
Если тебе нужно будет, то пришлю схему как рисовать таблицу, потому что она будет отличаться от обычной таблицы для графика функции
Всего три пары -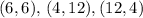
Объяснение:
Для того чтобы решить задачу, нужно правильно сформулировать проблему -
"Требуется найти все пары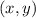
, где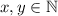 
так что 
."
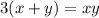Из равенства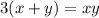
очевидно что 
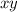делится на 3. Следовательно хотя бы одно из чисел 
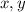делится на 3. Без огранчения общности, предположим что 
.
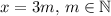Следовательно, высшеупомянотое равенство преообразовывается в
Заметим что отсюда выходит что,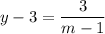
.
Т.к.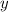
цело только и только тогда, когда 
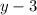цело, то следовательно, 3 должно делится на 
.
Число 3 делится только на четыре числа - 3, -3, 1, -1. Но лишь только два из них подходят - 3 и 1.
Следовательно,
Т.е.,
Отсюда получаем две пары -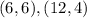
. Однако очевидно, что также и пара 
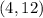подходит.
Дана функция y=-x^2 + 6x - 5.
График этой функции - парабола ветвями вниз.
Вершина параболы Хо = -в/2а = -6/-2 = 3,
Уо = -9+18-5 = 4.
Точки пересечения оси Ох:
-х² + 6х - 5 = 0,
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=6^2-4*(-1)*(-5)=36-4*(-1)*(-5)=36-(-4)*(-5)=36-(-4*(-5))=36-(-(-4*5))=36-(-(-20))=36-20=16;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√16-6)/(2*(-1))=(4-6)/(2*(-1))=-2/(2*(-1))=-2/(-2)=-(-2/2)=-(-1)=1;x₂=(-√16-6)/(2*(-1))=(-4-6)/(2*(-1))=-10/(2*(-1))=-10/(-2)=-(-10/2)=-(-5)=5.Точка пересечения оси Оу берётся из уравнения при х = 0, у = -5.
По графику (и по анализу) определяем:
1) промежуток убывания функции: х ∈ (3; ∞);
2) при каких значениях x функция принимает отрицательные значения:
х ∈ (-∞; 1) ∪ (5; +∞).
Объяснение:
Дана функция y=-x^2 + 6x - 5.
График этой функции - парабола ветвями вниз.
Вершина параболы Хо = -в/2а = -6/-2 = 3,
Уо = -9+18-5 = 4.
Точки пересечения оси Ох:
-х² + 6х - 5 = 0,
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=6^2-4*(-1)*(-5)=36-4*(-1)*(-5)=36-(-4)*(-5)=36-(-4*(-5))=36-(-(-4*5))=36-(-(-20))=36-20=16;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√16-6)/(2*(-1))=(4-6)/(2*(-1))=-2/(2*(-1))=-2/(-2)=-(-2/2)=-(-1)=1;x₂=(-√16-6)/(2*(-1))=(-4-6)/(2*(-1))=-10/(2*(-1))=-10/(-2)=-(-10/2)=-(-5)=5.Точка пересечения оси Оу берётся из уравнения при х = 0, у = -5.
По графику (и по анализу) определяем:
1) промежуток убывания функции: х ∈ (3; ∞);
2) при каких значениях x функция принимает отрицательные значения:
х ∈ (-∞; 1) ∪ (5; +∞).