Гражданин положил в банк определенную сумму денег под постоянный процент,расчитывая получить за год доход 900 тыс.рублей.через полгода ему пришлось снять со счета 400 тыс.рублей.какова была величина исходного
вклада,если в конце года сумма на счете составила 2 млн.рублей?
пусть изначальная сумма х руб.т.к 900тыс.прибыль за год,следовательно за 1мес. прибыль составляет 75тыс.,т.е 900000:6мес.=75000получаем,что прибыль за пол года составляет 450тыс.,т.е.6*75000=450000.но в задаче сказано,чточерез пол года ему пришлось снять со счета 400тыс.,следовательно прибыль составила всего 50тыс.,а т.к. на оставшуюся сумму по прежнему набегали проценты,то получаем,что х+50000+450000=2000000
х=1500000,по моему так.
Пусть х руб -- величина исходного вклада,
а y -- процент за месяц (выраженный в целом числе)
(xy^12) руб -- получил бы гражданин через год, если бы не снимал деньги
Т.к., если бы гражданин не снимал деньги, чистый доход за год был бы 900 тысяч руб, то можно составить уравнение:
xy^12=x+900000
(xy^6-400000) руб -- сбережения в банке спустя полгода
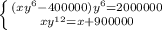
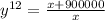
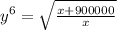
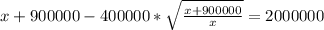
((xy^6-400000)y^6) руб -- сбережения в банке спустя год
Т.к. всего через год гражданин получил 2 миллиона, то можно составить урвнение:
(xy^6-400000)y^6=2000000
Составляем систему уравнений:
Берём второе уравнение и выражаем y^12:
Выражаем y^6
Упращаем первое выражение:
(xy^6-400000)y^6=2000000
xy^12-400000*y^6=2000000
Подстовляем второе преобразованное уравнение в первое преобразованное уравнение:
Находим х:
х=1600000
ответ: 1600000 рублей -- величина исходного вклада.