если не сложно можно на листочке
5.
Решите
графическим
методом
систему
уравнений:

у+1 = 2х
х+у= -4

2. найдите координаты точки пересечения функции ...(на фото функция) с осью абсцисс:

если не сложно можно на листочке5.Решитеграфическимметодомсистемууравнений:у+1 = 2хх+у= -42. найдите

Показать ответ

Ответ:

Dogi2008

26.12.2022 02:30

Объяснение:

решаю задачу с другим условием по согласованию с автором вопроса

Яке значення може приймати градусна міра кута а?

cos (x+a ) = - sin x

по формулам приведения мы знаем что косинус меняется на синус (и наоборот) если добавить угол равный 90 + 180*n

а если добавить угол равный 180*n может поменяться знак но функция не изменится

итак

косинус превратился в синус значит угол а это 90 или 270

при малом х синус положительный

по условию cos (x+a ) = - sin(x) - отрицательный

отрицательный косинус в 2 и 3 четверти

(x+a) должен лежать в 2 или 3 четверти

при малом х нам подходит либо 90 либо 180

смотрим ранее (90 или 270) и то что получили только что (90 или 180) и понимаем что ответ 90 - это ответ

0,0(0 оценок)

Ответ:

fd1132

29.11.2020 16:30

1) Проверим справедливость утверждения при n=1 :

$9^1 - 8\cdot1 - 1=9-8-1=0\ \vdots\ 16$

2) Предположим, что при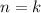 n=k утверждение справедливо, то есть:

$(9^k - 8k- 1)\ \vdots\ 16$

3) Докажем, что при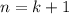 n=k+1 справедливо утверждение:

$\left(9^{k+1} - 8(k+1)- 1\right)\ \vdots\ 16$

Доказательство. Преобразуем:

$9^{k+1} - 8(k+1)- 1=9\cdot9^k - 8k-8- 1=$

$=(9^k- 8k-1)+8\cdot9^k -8=(9^k- 8k-1)+8(9^k -1)$

Первое слагаемое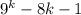 9^k- 8k-1 делится на 16 по предположению, сделанному на втором шаге.

$9^{k+1} - 8(k+1)- 1=\underset{\vdots\ 16}{\underbrace{(9^k- 8k-1)}}+8(9^k -1)$

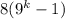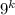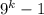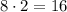Рассмотрим второе слагаемое 8(9^k -1) . Первый множитель 8 делится на 8. Заметим, что второй множитель является четным, так как выражение 9^k при $k\in\mathbb{N}$ дает нечетные числа, тогда числа вида 9^k -1 являются четными. Таким образом, второе слагаемое делится на $8\cdot2=16$ .