если частное двух целых чисел является целым - вопрос №14428097 от Ctypakelizaveta 15.04.2023 05:51

Question

Алгебра: если частное двух целых чисел является целым числом, делящимся на 6, то и делимое делится на 6. Да или нет? Приведите пример , если нет

Ctypakelizaveta · Answer

1) Проверим справедливость утверждения при n=1 :

$9^1 - 8\cdot1 - 1=9-8-1=0\ \vdots\ 16$

2) Предположим, что при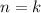 n=k утверждение справедливо, то есть:

$(9^k - 8k- 1)\ \vdots\ 16$

3) Докажем, что при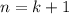 n=k+1 справедливо утверждение:

$\left(9^{k+1} - 8(k+1)- 1\right)\ \vdots\ 16$

Доказательство. Преобразуем:

$9^{k+1} - 8(k+1)- 1=9\cdot9^k - 8k-8- 1=$

$=(9^k- 8k-1)+8\cdot9^k -8=(9^k- 8k-1)+8(9^k -1)$

Первое слагаемое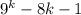 9^k- 8k-1 делится на 16 по предположению, сделанному на втором шаге.

$9^{k+1} - 8(k+1)- 1=\underset{\vdots\ 16}{\underbrace{(9^k- 8k-1)}}+8(9^k -1)$

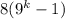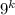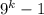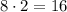Рассмотрим второе слагаемое 8(9^k -1) . Первый множитель 8 делится на 8. Заметим, что второй множитель является четным, так как выражение 9^k при $k\in\mathbb{N}$ дает нечетные числа, тогда числа вида 9^k -1 являются четными. Таким образом, второе слагаемое делится на $8\cdot2=16$ .

$9^{k+1} - 8(k+1)- 1=\underset{\vdots\ 16}{\underbrace{(9^k- 8k-1)}}+\underset{\vdots\ 16}{\underbrace{8(9^k -1)}}$

Итак, оба слагаемых делятся на 16. Значит и вся сумма делится на 16. Доказано.