за х км/час примем собственную скорость теплохода;
(х+2)км/час скорость теплохода по течению;
(х-2)км/час- скорость теплохода против течения;
126/(х+2)часов-время пути теплохода по течению;
126/(х-2)часов-время пути теплохода против течения.
В задаче сказано, что на путь туда и обратно и 8 часов остановки теплоход потратил сутки. Отсюда равенство: 126/(х+2)+126/(х-2)+8=24.
126(х+2)+126(х-2)=16(х+2)(х-2); 126х+252+126х-252=16(х^2-4);
16х^2-252х-64=0; 4х^2-63х-16=0. Решив это ур-ние через дискрименант, найдем х=16(км/час)-это собственная скорость теплохода.
Пусть х км/ч - скорость лодки;
у км/ч - скорость течения реки, тогда
(х+у) - скорость лодки по течению;
(х-у) - скорость лодки против течения.
По условию лодка путь от А до В Длиной 33 км туда и обратно проходит за 3 часа 20 мин.
3 часа 20 мин. = ¹⁰/₃ часа
Получаем первое уравнение:
По условию лодка на весь путь, который состоит из 11 км по течению и 9 км против течения, затратила 1 час.
Получаем второе уравнение:
ОДЗ: x>0; y>0; x≠y
Решаем систему:
{
1) Преобразуем первое уравнение:
2) Преобразуем второе уравнение:
3) Значение произведения (х-у)(х+у) из второго уравнения подставим в первое уравнение:
4) Подставим х=10у в первое уравнение 198x=10(x-y)(x+y).
не удовлетворяет ОДЗ
удовлетворяет ОДЗ
x=10y => х=2·10=20
ответ: 2 км/ч - скорость течения реки.
за х км/час примем собственную скорость теплохода;
(х+2)км/час скорость теплохода по течению;
(х-2)км/час- скорость теплохода против течения;
126/(х+2)часов-время пути теплохода по течению;
126/(х-2)часов-время пути теплохода против течения.
В задаче сказано, что на путь туда и обратно и 8 часов остановки теплоход потратил сутки. Отсюда равенство: 126/(х+2)+126/(х-2)+8=24.
126(х+2)+126(х-2)=16(х+2)(х-2); 126х+252+126х-252=16(х^2-4);
16х^2-252х-64=0; 4х^2-63х-16=0. Решив это ур-ние через дискрименант, найдем х=16(км/час)-это собственная скорость теплохода.
Пусть х км/ч - скорость лодки;
у км/ч - скорость течения реки, тогда
(х+у) - скорость лодки по течению;
(х-у) - скорость лодки против течения.
По условию лодка путь от А до В Длиной 33 км туда и обратно проходит за 3 часа 20 мин.
3 часа 20 мин. = ¹⁰/₃ часа
Получаем первое уравнение:
По условию лодка на весь путь, который состоит из 11 км по течению и 9 км против течения, затратила 1 час.
Получаем второе уравнение:
ОДЗ: x>0; y>0; x≠y
Решаем систему:
{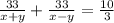
{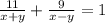
1) Преобразуем первое уравнение:
2) Преобразуем второе уравнение:
3) Значение произведения (х-у)(х+у) из второго уравнения подставим в первое уравнение:
4) Подставим х=10у в первое уравнение 198x=10(x-y)(x+y).
x=10y => х=2·10=20
ответ: 2 км/ч - скорость течения реки.