(x-1)(x+3)(x-2)(+1)<0
Рассмотрим все возможные случаи
затем найдем пересечение
в 1 случае
это х∈(-∞;-3)∪(1;2)
а во 2 случае
х∈∅
Находим объединение
Объяснение:
(x-1)(x+3)(x-2)(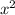 +1)<0
+1)<0
Рассмотрим все возможные случаи
затем найдем пересечение
в 1 случае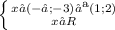
это х∈(-∞;-3)∪(1;2)
а во 2 случае
х∈∅
Находим объединение
это х∈(-∞;-3)∪(1;2)
Объяснение: