Довести що 10 а ^-6а -2ав+в^+2 більше 0 для всіх дійсних значень а і в

Число р при делении на 3 может давать остатки 0,1 или 2.

Если число р при делении на 3 дает остаток 1, то оно имеет вид

p=3k+1, где k - некоторое целое число

Но тогда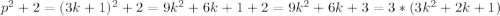 , а значит число 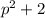не является простым. Значит такой случай невозможен

Если число р при делении на 3 дает остаток 2, то оно имеет вид

p=3k+2, где k - некоторое целое число

Но тогда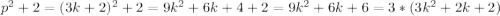 , а значит число 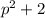не является простым. Значит такой случай невозможен

Значит число р при делении на 3 дает остаток 0, а значит число р делится нацело на 3. Число р делится нацело на 3 и является простым, значит число р может равняться только числу 3.

При р=3: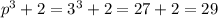 - простое, что и требовалось доказать.Доказано

1.  2-6,72:2,4=2-2,8= -0,8

2. 8×(-2,6)-3,7=-20,8-3,7=-24,5

3. 0.4(x-5y)+1.5(2x-y)=0.4x-2y+3x-1.5y=3.4x-3.5y

c-(3c-(5c-1))=c-(3c-5c+1)=c-3c+5c-1=3c-1

c=1/3

4. а) 5x - 0.8 = 2x + 1.6;

5x - 2x = 1.6 + 0.8;

x(5 - 2) = 2.4;

3x = 2.4;

x = 2.4 : 3;

x = 0.8.

б) 4 - 2(x + 3) = 4(x - 5);

4 - 2 * x - 2 * 3 = 4 * x - 4 * 5;

4 - 2x - 6 = 4x - 20;

-2x - 4x = -20 - 4 + 6;

x(-2 - 4) = -18;

-6x = -18;

x = -18 : (-6);

x = 3

5.  6 * X = 4 * ( X + 5 ) ;

6 * X = 4 * X + 20 ;

2 * X = 20 ;

X = 10 ;

10 деталей изготавливал ученик, а мастер изготавливал 10 + 5 = 15 деталей.

6.  2 * х - 5 = (х - 10) * 3,

2 * х - 5 = 3 * х - 30,

х = 30 - 5,

х = 25 (кг) - было во втором ящике, значит в первом было 2 * 25 = 50 кг гвоздей.

ответ: 50 кг и 25 кг.