Обозначим число вагонов, в которых свободна половина мест, и - число вагонов, в которых свободна треть мест.
Тогда . Получаем три решения:
1) ;
2) ;
3) .
Решения 1) и 3) не подходят, так как по условию имеются и вагоны, в которых свободна половина мест и такие, в которых свободна треть мест. Остаётся решение 2), т.е. в трёх вагонах было свободно по трети мест и в двух вагонах - свободно по половине мест.
Значит, всего вагонов со свободными местами было . А полностью занятых выгонов ехало .
ответы : 1) два числа в сумме дают 3, а при умножении 2, значит это числа 2 и 1.
2) в сумме - 30, а при умножении 225, 225 это 15 *15, значит корни - 15 и - 15.
3) в сумме 22, при умножении 105, это могут дать только 15 и 7.
4) в сумме - 29, при умножении 180, это числа - 20 и - 9. (можно и через дискриминант, но я могу и такие числа подобрать, это не сложно.)
5)здесь надёжнее для всех решать через дискриминант, в этом примере он равен 441, значит это 21^2. x1=(-3-21)/2=-12
x2=(-3+21)/2=9
Корни этого уравнения : - 12 и 9.
6)в этом примере также лучше решать через дискриминант, но числа лёгкие для подбора, они в сумме равны - 3, а в произведении - 340, значит это - 20 и 17.
7)в сумме 1, в произведении - 72, значит это - 8 и 9.
8)в сумме - 5, в произведении - 66, такое могут дать только - 11 и 6.
9)в сумме 36, а в произведении 324, это же 18 ^2, сразу вспоминается таблица квадратов. Итак, корни 18 и 18. Можно написать в ответ только один корень, потому что они одинаковые.
10) в сумме 11, в произведении 24, это 8 и 3.
11) в сумме 10, в произведении 9, корни этого уравнения 9 и 1.
12)в сумме 30, при умножении 209, из этого можно понять что это 19 и 11.
13)в сумме 6, при умножении - 135, значит корни 15 и - 9.
14)в сумме 5, при умножении -150, корни 15 и -10.
15) в сумме - 9, при умножении - 190, значит корни -19 и 10.
Объяснение:
Теорема виета служит для быстрого решения уравнений подбором. ax^2+px+q=0
-p=x1+x2(здесь мы берём противоположное число тому, что стоит перед x.)
ответ: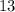
.
Объяснение:
Обозначим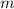
число вагонов, в которых свободна половина мест, и 
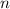- число вагонов, в которых свободна треть мест.
Тогда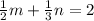
. Получаем три решения:
1)
;
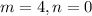2)
;
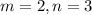3)
.
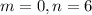Решения 1) и 3) не подходят, так как по условию имеются и вагоны, в которых свободна половина мест и такие, в которых свободна треть мест. Остаётся решение 2), т.е. в трёх вагонах было свободно по трети мест и в двух вагонах - свободно по половине мест.
Значит, всего вагонов со свободными местами было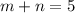
. А полностью занятых выгонов ехало 
.
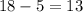ответы : 1) два числа в сумме дают 3, а при умножении 2, значит это числа 2 и 1.
2) в сумме - 30, а при умножении 225, 225 это 15 *15, значит корни - 15 и - 15.
3) в сумме 22, при умножении 105, это могут дать только 15 и 7.
4) в сумме - 29, при умножении 180, это числа - 20 и - 9. (можно и через дискриминант, но я могу и такие числа подобрать, это не сложно.)
5)здесь надёжнее для всех решать через дискриминант, в этом примере он равен 441, значит это 21^2. x1=(-3-21)/2=-12
x2=(-3+21)/2=9
Корни этого уравнения : - 12 и 9.
6)в этом примере также лучше решать через дискриминант, но числа лёгкие для подбора, они в сумме равны - 3, а в произведении - 340, значит это - 20 и 17.
7)в сумме 1, в произведении - 72, значит это - 8 и 9.
8)в сумме - 5, в произведении - 66, такое могут дать только - 11 и 6.
9)в сумме 36, а в произведении 324, это же 18 ^2, сразу вспоминается таблица квадратов. Итак, корни 18 и 18. Можно написать в ответ только один корень, потому что они одинаковые.
10) в сумме 11, в произведении 24, это 8 и 3.
11) в сумме 10, в произведении 9, корни этого уравнения 9 и 1.
12)в сумме 30, при умножении 209, из этого можно понять что это 19 и 11.
13)в сумме 6, при умножении - 135, значит корни 15 и - 9.
14)в сумме 5, при умножении -150, корни 15 и -10.
15) в сумме - 9, при умножении - 190, значит корни -19 и 10.
Объяснение:
Теорема виета служит для быстрого решения уравнений подбором. ax^2+px+q=0
-p=x1+x2(здесь мы берём противоположное число тому, что стоит перед x.)
q=x1*x2