В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение:
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части:
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень
На первый взгляд задача очень простая. Зачастую решение таких задач сводят к нахождению объемов параллелепипедов и затем объём большего делят на объём меньшего ( как, кстати, и задач на количество плиток одной площади по поверхности большей площади). Переводим размеры в одинаковые единицы измерения Для кузова машины 32дм, 32 дм и 80 дм для коробок 4 дм, 8 дм и 10 дм V1:V2=(32•32•80):(4•8•10)=8•4•8=256 (коробок)
НО! Следует заметить, что объёмы могут делиться нацело, а полученное от деления количество коробок не поместится в кузове, т.к. их размеры могут не быть кратными. На рисунке приложения показан оптимальный вариант размещения коробок. По условию этой задачи коробки можно разместить в кузове без зазоров, они полностью займут его пространство, т.к. размеры коробки помещается по длине кузова 80:10=8 раз, по ширине 32:8=4 раза и по высоте 32:4=8 раз. Всего поместится 8•8•4=256 коробок. Если размещать их длиной по высоте кузова, получим три слоя коробок–32:10=3 (два дм высоты останутся незаполненными). Тогда поместится 20•4•3=240 коробок. Всегда следует высчитывать, сколько раз умещаются размеры меньшей фигуры в размерах большей.
В иррациональных уравнениях кроме ОДЗ нужно всегда учитывать дополнительные условия (ДУ) или всегда для проверки подставлять полученные корни в исходное уравнение.
Рассмотрим исходное уравнение: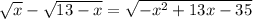
Далее мы возводим это уравнение в квадрат, но это неэквивалентный переход - например, неправильное равенство -1 = 1 переходит в правильное 1 = 1, поэтому на этом этапе легко приобрести лишние корни, что и произошло.
В правой части исходного уравнения находится неотрицательный корень, поэтому в ДУ необходимо потребовать неотрицательность левой части: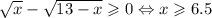
Как раз это ДУ и позволяет в процессе решения откинуть лишний корень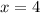
Зачастую решение таких задач сводят к нахождению объемов параллелепипедов и затем объём большего делят на объём меньшего ( как, кстати, и задач на количество плиток одной площади по поверхности большей площади).
Переводим размеры в одинаковые единицы измерения
Для кузова машины 32дм, 32 дм и 80 дм
для коробок 4 дм, 8 дм и 10 дм
V1:V2=(32•32•80):(4•8•10)=8•4•8=256 (коробок)
НО! Следует заметить, что объёмы могут делиться нацело, а полученное от деления количество коробок не поместится в кузове, т.к. их размеры могут не быть кратными.
На рисунке приложения показан оптимальный вариант размещения коробок.
По условию этой задачи коробки можно разместить в кузове без зазоров, они полностью займут его пространство, т.к. размеры коробки помещается по длине кузова 80:10=8 раз, по ширине 32:8=4 раза и по высоте 32:4=8 раз. Всего поместится 8•8•4=256 коробок.
Если размещать их длиной по высоте кузова, получим три слоя коробок–32:10=3 (два дм высоты останутся незаполненными). Тогда поместится 20•4•3=240 коробок.
Всегда следует высчитывать, сколько раз умещаются размеры меньшей фигуры в размерах большей.